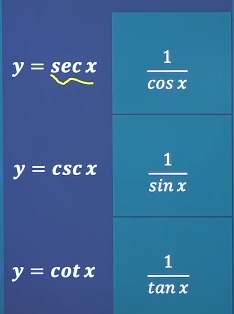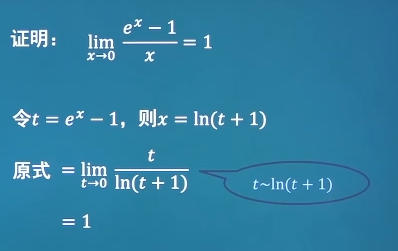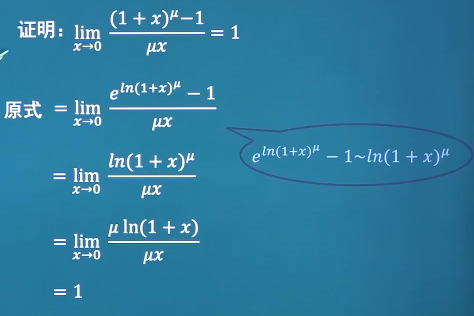一.函数、极限与连续 函数 函数三要素: 自变量(x),因变量(y),对应法则;
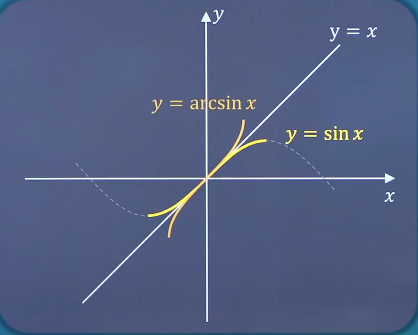
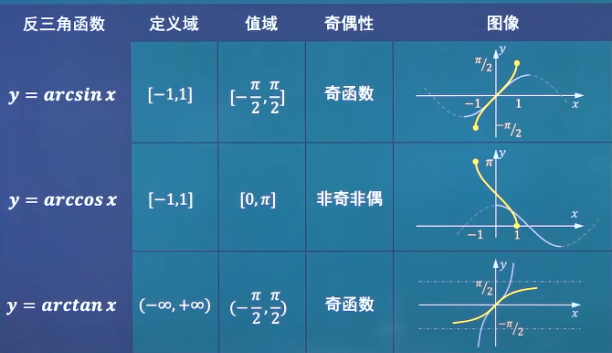
定义域及值域 自然定义域:s i n x ; sinx; s i n x ; c o s x → R ( 定义域 ) ; cosx \to R(定义域); c o s x → R ( 定 义 域 ) ; 1 x → ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) ; \frac{1}{x} \to (-\infty, 0) \cup (0, +\infty); x 1 → ( − ∞ , 0 ) ∪ ( 0 , + ∞ ) ; x → [ 0 , + ∞ ) ; \sqrt {x} \to [0, +\infty); x → [ 0 , + ∞ ) ; l o g a x → [ 0 , + ∞ ) log_ax \to [0, +\infty) l o g a x → [ 0 , + ∞ ) t a n x → x ∣ x ≠ π 2 + k π , k ∈ Z tan x \to{x|x\neq\frac{\pi}{2}+k\pi,k∈Z} t a n x → x ∣ x = 2 π + k π , k ∈ Z arcsin x → [ − 1 , 1 ] \arcsin x \to [-1,1] arcsin x → [ − 1 , 1 ] arccos x → [ − 1 , 1 ] \arccos x \to [-1,1] arccos x → [ − 1 , 1 ]
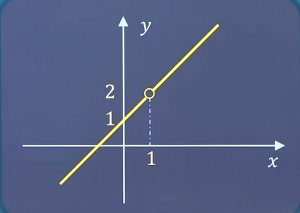
判断两个函数是否为同一个函数 二者同时满足<——(充要条件)——>两函数为同一函数y 1 = x 2 y_1=\sqrt{x^2} y 1 = x 2 y 2 = ∣ x ∣ y_2=|x| y 2 = ∣ x ∣ x 2 ≥ 0 = > x ∈ R x^2\geq0=>x∈R x 2 ≥ 0 = > x ∈ R x ∈ R x∈R x ∈ R y 1 = x 2 = { x , x ≥ 0 − x , x < 0 y_1=\sqrt{x^2}=\begin{cases} x,x\geq0\\\\-x,x<0 \end{cases} y 1 = x 2 = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x , x ≥ 0 − x , x < 0 y 2 = ∣ x ∣ = { x , x ≥ 0 − x , x < 0 y_2=|x|=\begin{cases}x,x\geq0 \\\\-x,x<0\end{cases} y 2 = ∣ x ∣ = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ x , x ≥ 0 − x , x < 0 是*同一函数f ( x ) = x + 1 f(x)=x+1 f ( x ) = x + 1 g ( x ) = x 2 − 1 x − 1 g(x)=\frac{x^2-1}{x-1} g ( x ) = x − 1 x 2 − 1 x x x f ( x ) = sin x —— R ( f ) + − 都存在 , g ( x ) = 1 − cos 2 x 2 —— R ( f ) f(x)=\sin x——R(f)+-都存在,g(x)=\sqrt{\frac{1-\cos 2x}{2}}—— R(f) f ( x ) = sin x — — R ( f ) + − 都 存 在 , g ( x ) = 2 1 − c o s 2 x — — R ( f ) f ( x ) = 1 x f(x)=\frac{1}{x} f ( x ) = x 1 x x x g ( x ) = 1 [ x ] 2 g(x)=\frac{1}{[\sqrt{x}]^2} g ( x ) = [ x ] 2 1 f ( x ) = x + 1 f(x)=x+1 f ( x ) = x + 1 g ( t ) = t + 1 g(t)=t+1 g ( t ) = t + 1
特殊函数 1.分段函数隐函数 参数方程式 抽象函数 y = f ( x ) y=f(x) y = f ( x ) y = f ( x − 2 ) y=f(x-2) y = f ( x − 2 ) ∵ f ( x ) \because f(x) ∵ f ( x ) ∴ − 1 ≤ x < 1 \therefore-1\leq x<1 ∴ − 1 ≤ x < 1 ∴ − 1 ≤ x < 1 \therefore -1 \leq x<1 ∴ − 1 ≤ x < 1 1 ≤ x < 3 1 \leq x<3 1 ≤ x < 3
例题:已知函数y = f ( 2 x + 3 ) y=f(2x+3) y = f ( 2 x + 3 ) y = f ( 1 2 x − 5 ) y=f(\frac{1}{2}x-5) y = f ( 2 1 x − 5 ) ∵ f ( x ) \because f(x) ∵ f ( x ) − 2 < x ≤ 2 -2<x\leq 2 − 2 < x ≤ 2 ∴ − 1 < 2 x + 3 ≤ 7 \therefore-1< 2x+3 \leq7 ∴ − 1 < 2 x + 3 ≤ 7 ∴ − 1 < 1 2 x − 5 ≤ 7 \therefore -1 < \frac{1}{2}x-5\leq7 ∴ − 1 < 2 1 x − 5 ≤ 7 8 < x ≤ 24 8 < x\leq24 8 < x ≤ 2 4 4.2求抽象函数的表达式f ( x ) = x 2 + 2 x f(x)=x^2+2x f ( x ) = x 2 + 2 x f ( x 2 + 1 ) f(\frac{x}{2}+1) f ( 2 x + 1 ) f ( x 2 + 1 ) = x 2 4 + 2 x + 3 f(\frac{x}{2}+1)=\frac{x^2}{4}+2x+3 f ( 2 x + 1 ) = 4 x 2 + 2 x + 3 直接代入法∵ f ( x ) = x 2 + 2 x \because f(x)=x^2+2x ∵ f ( x ) = x 2 + 2 x f ( t ) = t 2 + 2 t f(t)=t^2+2t f ( t ) = t 2 + 2 t ∴ f ( x 2 + 1 ) = ( x 2 + 1 ) 2 + 2 ( x 2 + 1 ) \therefore f(\frac{x}{2}+1)=(\frac{x}{2}+1)^2+2(\frac{x}{2}+1) ∴ f ( 2 x + 1 ) = ( 2 x + 1 ) 2 + 2 ( 2 x + 1 ) ∴ f ( x 2 + 1 ) = x 2 4 + 2 x + 3 \therefore f(\frac{x}{2}+1)=\frac{x^2}{4}+2x+3 ∴ f ( 2 x + 1 ) = 4 x 2 + 2 x + 3 f ( x 2 + 1 ) = x 2 + 2 x f(\frac{x}{2}+1)=x^2+2x f ( 2 x + 1 ) = x 2 + 2 x f ( x ) f(x) f ( x ) f ( x ) = 4 x 2 − 4 x f(x)=4x^2-4x f ( x ) = 4 x 2 − 4 x x 2 + 1 = t \frac{x}{2}+1=t 2 x + 1 = t x = 2 t − 2 x=2t-2 x = 2 t − 2 ∴ f ( t ) = ( 2 t − 2 ) 2 + 2 ( t − 2 ) \therefore f(t)=(2t-2)^2+2(t-2) ∴ f ( t ) = ( 2 t − 2 ) 2 + 2 ( t − 2 ) ∴ f ( t ) = 4 t 2 − 4 t \therefore f(t)=4t^2-4t ∴ f ( t ) = 4 t 2 − 4 t f ( x ) = 4 x 2 − 4 x f(x)=4x^2-4x f ( x ) = 4 x 2 − 4 x f ( x 2 + 1 ) = x 2 + 2 x f(\frac{x}{2}+1)=x^2+2x f ( 2 x + 1 ) = x 2 + 2 x f ( 2 x − 1 ) f(2x-1) f ( 2 x − 1 ) f ( 2 x − 1 ) = 16 x 2 − 16 x + 8 f(2x-1)=16x^2-16x+8 f ( 2 x − 1 ) = 1 6 x 2 − 1 6 x + 8 x 2 + 1 = t \frac{x}{2}+1=t 2 x + 1 = t x = 2 t − 2 x=2t-2 x = 2 t − 2 ∴ f ( t ) = ( 2 t − 2 ) 2 + 2 ( t − 2 ) \therefore f(t)=(2t-2)^2+2(t-2) ∴ f ( t ) = ( 2 t − 2 ) 2 + 2 ( t − 2 ) ∴ f ( t ) = 4 t 2 − 4 t \therefore f(t)=4t^2-4t ∴ f ( t ) = 4 t 2 − 4 t f ( x ) = 4 x 2 − 4 x f(x)=4x^2-4x f ( x ) = 4 x 2 − 4 x ∴ f ( 2 x − 1 ) = 4 ( 2 x − 1 ) 2 − 4 ( 2 x − 1 ) \therefore f(2x-1)=4(2x-1)^2-4(2x-1) ∴ f ( 2 x − 1 ) = 4 ( 2 x − 1 ) 2 − 4 ( 2 x − 1 ) f ( 2 x − 1 ) = 16 x 2 − 16 x + 8 f(2x-1)=16x^2-16x+8 f ( 2 x − 1 ) = 1 6 x 2 − 1 6 x + 8
函数的基本特性 有界性 函数在f ( x ) f(x) f ( x ) 恒 ≥某数K 1 K_1 K 1 有下界 ,K 1 K_1 K 1 f ( x ) f(x) f ( x ) f ( x ) f(x) f ( x ) 恒 ≤某数K 2 K_2 K 2 有上界 ,K 2 K_2 K 2 f ( x ) f(x) f ( x ) 上界下界同时存在 ,则称函数f ( x ) f(x) f ( x ) 有界 ,有∣ f ( x ) ∣ ≤ M ( M > 0 ) |f(x)|\leq M(M>0) ∣ f ( x ) ∣ ≤ M ( M > 0 ) f ( x ) f(x) f ( x ) y = x 2 y=x^2 y = x 2 [ 0 , + ∞ ) [0,+\infty) [ 0 , + ∞ ) y = sin x → [ − 1 , 1 ] y=\sin x \to [-1,1] y = sin x → [ − 1 , 1 ] y = cos x → [ − 1 , 1 ] y=\cos x \to [-1,1] y = cos x → [ − 1 , 1 ] y = tan x → ( − ∞ , + ∞ ) y=\tan x \to (-\infty,+\infty) y = tan x → ( − ∞ , + ∞ )
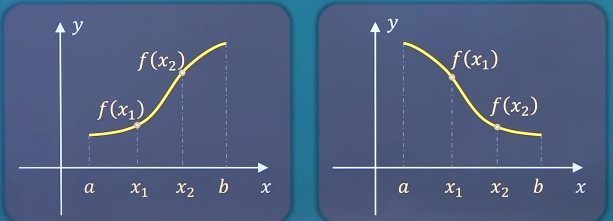
单调性 设函数f ( x ) f(x) f ( x ) x 1 , x 2 ∈ ( a , b ) x_1,x_2∈(a,b) x 1 , x 2 ∈ ( a , b ) f ( x 1 ) f(x_1) f ( x 1 ) f ( x 2 ) f(x_2) f ( x 2 ) f ( x ) f(x) f ( x ) f ( x 1 ) f(x_1) f ( x 1 ) f ( x 2 ) f(x_2) f ( x 2 ) f ( x ) f(x) f ( x ) 单增单减 y = x 1 − x y=\frac{x}{1-x} y = 1 − x x ( − ∞ , 1 ) (-\infty,1) ( − ∞ , 1 ) ( − ∞ , 1 ) (-\infty,1) ( − ∞ , 1 ) ∀ \forall ∀ x 1 , x 2 x_1,x_2 x 1 , x 2 x 1 < x 2 x_1<x_2 x 1 < x 2 f ( x 1 ) − f ( x 2 ) = x 1 1 − x 1 − x 2 1 − x 2 f(x_1)-f(x_2)=\frac{x_1}{1-x_1}-\frac{x_2}{1-x_2} f ( x 1 ) − f ( x 2 ) = 1 − x 1 x 1 − 1 − x 2 x 2 f ( x 1 ) − f ( x 2 ) = x 1 − x 2 ( 1 − x 1 ) ( 1 − x 2 ) f(x_1)-f(x_2)=\frac{x_1-x_2}{(1-x_1)(1-x_2)} f ( x 1 ) − f ( x 2 ) = ( 1 − x 1 ) ( 1 − x 2 ) x 1 − x 2 ∵ \because ∵ ( − ∞ , 1 ) (-\infty,1) ( − ∞ , 1 ) ∴ \therefore ∴ ( 1 − x 1 ) ( 1 − x 2 ) > 0 (1-x_1)(1-x_2)>0 ( 1 − x 1 ) ( 1 − x 2 ) > 0 x 1 − x 2 < 0 x_1-x_2<0 x 1 − x 2 < 0 ∴ \therefore ∴ f ( x 1 ) − f ( x 2 ) < 0 f(x_1)-f(x_2)<0 f ( x 1 ) − f ( x 2 ) < 0 ∴ f ( x 1 ) < f ( x 2 ) \therefore f(x_1)<f(x_2) ∴ f ( x 1 ) < f ( x 2 ) ∵ f ( x 1 ) \because f(x_1) ∵ f ( x 1 ) < f ( x 2 ) <f(x_2) < f ( x 2 ) ∴ \therefore ∴ ( − ∞ , 1 ) (-\infty,1) ( − ∞ , 1 )
奇偶性 设函数y = f ( x ) y=f(x) y = f ( x ) x ∈ D x∈D x ∈ D f ( − x ) = f ( x ) f(-x)=f(x) f ( − x ) = f ( x ) f ( x ) f(x) f ( x ) f ( − x ) = − f ( x ) f(-x)=-f(x) f ( − x ) = − f ( x ) f ( x ) f(x) f ( x ) y y y 轴 对称,奇函数关于原点 对称。奇函数+奇函数=奇函数 偶函数+偶函数=偶函数 奇函数+偶函数=非奇非偶函数 奇函数× \times × 偶函数× \times × 奇函数× \times ×
规律: 1.如果一个函数是奇函数或者偶函数,首先应该满足的条件是其定义域关于原点对称,如果定义域关于原点不对称,那么该函数肯定既不是奇函数也不是偶函数奇函数 在x = 0 x=0 x = 0 f ( 0 ) = 0 f(0)=0 f ( 0 ) = 0
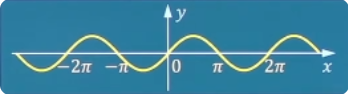
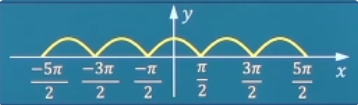
周期性 设函数y = f ( x ) y=f(x) y = f ( x ) T > 0 T>0 T > 0 x ∈ D x∈D x ∈ D x ± T ∈ D x\pm T∈D x ± T ∈ D f ( x ± T ) = f ( x ) f(x\pm T)=f(x) f ( x ± T ) = f ( x ) f ( x ) f(x) f ( x ) 周期函数 。f ( x ) f(x) f ( x ) 最小正周期 。
函数
图像表达式
周期
最小正周期
y = sin x y=\sin x y = sin x sinx 2 k π , k ∈ z 2k\pi,k∈z 2 k π , k ∈ z 2 π 2\pi 2 π
y = ∣ cos x ∣ y=|\cos x| y = ∣ cos x ∣ cosx k π , k ∈ z k\pi,k∈z k π , k ∈ z π \pi π
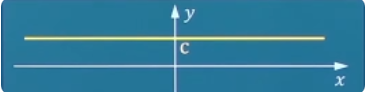
常值函数y = c y=c y = c
常值函数 任何正有理数
不存在
狄利克雷函数
y = { 1 , x ∈ Q 0 , x ∈ Q c y=\begin{cases} 1, x∈Q \\\\0,x∈Q^c\end{cases} y = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 1 , x ∈ Q 0 , x ∈ Q c 任何正有理数
不存在
反函数与复合函数 把原函数y = f ( x ) y=f(x) y = f ( x ) x = f − ( y ) x=f^-(y) x = f − ( y ) y = 2 x , x ∈ ( 0 , 1 ) y=2x,x∈(0,1) y = 2 x , x ∈ ( 0 , 1 ) x = 1 2 y , y ∈ ( 0 , 2 ) x=\frac{1}{2}y,y∈(0,2) x = 2 1 y , y ∈ ( 0 , 2 ) y = 1 2 x , x ∈ ( 0 , 2 ) y=\frac{1}{2}x,x∈(0,2) y = 2 1 x , x ∈ ( 0 , 2 ) y = x 2 y=x^2 y = x 2 y = s i n x y=sinx y = s i n x x ∈ R x∈R x ∈ R
反函数的性质 反函数和原函数的图像关于直线y = x y=x y = x
反函数和原函数单调性相同。
复合函数 自变量x x x u = g ( x ) u=g(x) u = g ( x ) u u u y = f ( u ) y=f(u) y = f ( u ) y y y y = f ( u ) y=f(u) y = f ( u ) u = g ( x ) u=g(x) u = g ( x ) y = f [ g ( x ) ] y=f[g(x)] y = f [ g ( x ) ]
注意复合的先后次序,y = f [ g ( x ) ] y=f[g(x)] y = f [ g ( x ) ] y = g [ f ( x ) ] y=g[f(x)] y = g [ f ( x ) ]
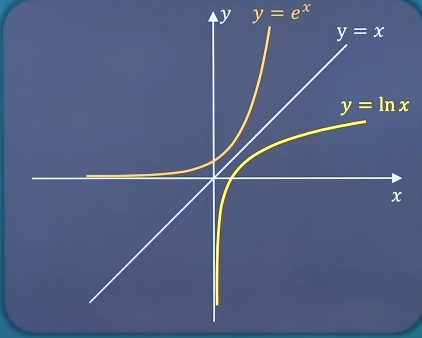
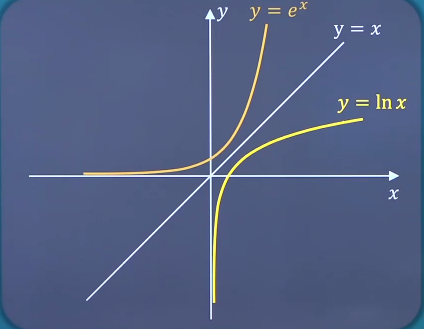
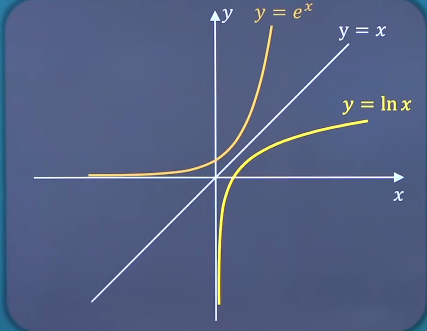
内层函数u = g ( x ) u=g(x) u = g ( x ) y = f ( u ) y=f(u) y = f ( u ) 基本初等函数(五类) 幂函数、指数函数、对数函数、三角函数、反三角函数通称基本初等函数。幂函数:y = x μ y=x^\mu y = x μ μ ∈ R \mu∈R μ ∈ R 定义域和值域随μ \mu μ 0 , + ∞ 0,+\infty 0 , + ∞ 指数函数:y = a x y=a^x y = a x a > 0 , a ≠ 1 a>0,a\ne1 a > 0 , a = 1 特别当a = e a=e a = e y = e x y=e^x y = e x e ≈ 2.718 e\approx2.718 e ≈ 2 . 7 1 8 对数函数:y = l o g a x y=log_ax y = l o g a x a > 0 , a ≠ 1 a>0,a\ne1 a > 0 , a = 1 特别当a = e a=e a = e y = l n x y=lnx y = l n x 三角函数 反三角函数
极限 数列 数列的概念 一列有规律的数,对每个n ∈ N + n\in N_+ n ∈ N + x n {x_n} x n 数列一定是有无穷多项
数列极限的概念 对于数列x n {x_n} x n ∀ ε > 0 \forall \varepsilon>0 ∀ ε > 0 ∃ \exists ∃ N N N n > N n>N n > N ∣ x n − a ∣ < ε |x_n-a|< \varepsilon ∣ x n − a ∣ < ε a a a x n {x_n} x n x n {x_n} x n a a a lim n → + ∞ x n = a \lim_{n\rightarrow+\infty}{x_n}=a lim n → + ∞ x n = a
收敛数列->有极限的数列的性质
收敛数列必有极限,且极限唯一;
收敛数列一定有界;
有界数列不一定收敛(例 ( − 1 ) n ) (例{(-1)^n}) ( 例 ( − 1 ) n )
夹逼准则 * 对于三个数列y n 、 x n 、 z n {y_n}、{x_n}、{z_n} y n 、 x n 、 z n y n < x n < z n y_n<x_n<z_n y n < x n < z n lim n → ∞ y n = a ,且 lim n → ∞ z n = a \lim_{n\rightarrow\infty}{y_n}=a,且\lim_{n\rightarrow\infty}{z_n}=a lim n → ∞ y n = a , 且 lim n → ∞ z n = a lim n → ∞ x n = a \lim_{n\rightarrow\infty}{x_n}=a lim n → ∞ x n = a lim n → ∞ ( 1 n 2 + 1 + 1 n 2 + 2 + ⋅ ⋅ ⋅ + 1 n 2 + n ) \lim_{n\rightarrow\infty}{(\frac{1}{n^2+1}+\frac{1}{n^2+2}+···+\frac{1}{n^2+n})} lim n → ∞ ( n 2 + 1 1 + n 2 + 2 1 + ⋅ ⋅ ⋅ + n 2 + n 1 ) n n n x n x_n x n y n y_n y n z n z_n z n y n y_n y n z n z_n z n y n = ( 1 n 2 + n + 1 n 2 + n + ⋅ ⋅ ⋅ + 1 n 2 + n ) = n n 2 + n = 1 n + 1 y_n=(\frac{1}{n^2+n}+\frac{1}{n^2+n}+···+\frac{1}{n^2+n})=\frac{n}{n^2+n}=\frac{1}{n+1} y n = ( n 2 + n 1 + n 2 + n 1 + ⋅ ⋅ ⋅ + n 2 + n 1 ) = n 2 + n n = n + 1 1 z n = ( 1 n 2 + 1 + 1 n 2 + 1 + ⋅ ⋅ ⋅ + 1 n 2 + 1 ) = n n 2 + 1 z_n=(\frac{1}{n^2+1}+\frac{1}{n^2+1}+···+\frac{1}{n^2+1})=\frac{n}{n^2+1} z n = ( n 2 + 1 1 + n 2 + 1 1 + ⋅ ⋅ ⋅ + n 2 + 1 1 ) = n 2 + 1 n lim n → ∞ y n = lim n → ∞ 1 n + 1 = 0 \lim_{n\rightarrow\infty}y_n=\lim_{n\rightarrow\infty}{\frac{1}{n+1}}=0 lim n → ∞ y n = lim n → ∞ n + 1 1 = 0 lim n → ∞ z n = lim n → ∞ n n 2 + n = 0 \lim_{n\rightarrow\infty}z_n=\lim_{n\rightarrow\infty}{\frac{n}{n^2+n}}=0 lim n → ∞ z n = lim n → ∞ n 2 + n n = 0
求极限:lim n → ∞ ( 1 n 2 + n + 1 + 2 n 2 + n + 2 + ⋅ ⋅ ⋅ + n n 2 + n + n ) \lim_{n\rightarrow\infty}{(\frac{1}{n^2+n+1}+\frac{2}{n^2+n+2}+···+\frac{n}{n^2+n+n})} lim n → ∞ ( n 2 + n + 1 1 + n 2 + n + 2 2 + ⋅ ⋅ ⋅ + n 2 + n + n n ) y n = ( 1 n 2 + n + n + 2 n 2 + n + n + ⋅ ⋅ ⋅ + n n 2 + n + n ) = 1 2 ( n + 1 ) n 2 + n + n = n 2 + n 2 n 2 + 4 n y_n=(\frac{1}{n^2+n+n}+\frac{2}{n^2+n+n}+···+\frac{n}{n^2+n+n})=\frac{\frac{1}{2}(n+1)}{n^2+n+n}=\frac{n^2+n}{2n^2+4n} y n = ( n 2 + n + n 1 + n 2 + n + n 2 + ⋅ ⋅ ⋅ + n 2 + n + n n ) = n 2 + n + n 2 1 ( n + 1 ) = 2 n 2 + 4 n n 2 + n z n = ( 1 n 2 + n + 1 + 2 n 2 + n + 1 + ⋅ ⋅ ⋅ + n n 2 + n + 1 ) = 1 2 n ( n 2 + 1 ) n 2 + n + 1 = 1 + 1 n 2 + 1 n + 1 n z_n=(\frac{1}{n^2+n+1}+\frac{2}{n^2+n+1}+···+\frac{n}{n^2+n+1})=\frac{\frac{1}{2}n(n^2+1)}{n^2+n+1}=\frac{1+\frac{1}{n}}{2+\frac{1}{n}+\frac{1}{n}} z n = ( n 2 + n + 1 1 + n 2 + n + 1 2 + ⋅ ⋅ ⋅ + n 2 + n + 1 n ) = n 2 + n + 1 2 1 n ( n 2 + 1 ) = 2 + n 1 + n 1 1 + n 1 lim n → ∞ y n = n 2 + n 2 n 2 + 4 n = 1 2 \lim_{n\rightarrow\infty}{y_n}=\frac{n^2+n}{2n^2+4n}=\frac{1}{2} lim n → ∞ y n = 2 n 2 + 4 n n 2 + n = 2 1 lim n → ∞ z n = 1 + 1 n 2 + 1 n + 1 n = 1 2 \lim_{n\rightarrow\infty}{z_n}=\frac{1+\frac{1}{n}}{2+\frac{1}{n}+\frac{1}{n}}=\frac{1}{2} lim n → ∞ z n = 2 + n 1 + n 1 1 + n 1 = 2 1
课后练习:lim n → ∞ ( 1 n 2 + 1 + 1 n 2 + 2 + ⋯ + 1 n 2 + n ) \lim_{n\rightarrow\infty}{(\frac{1}{\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+2}}+\cdots+\frac{1}{\sqrt{n^2+n}})} lim n → ∞ ( n 2 + 1 1 + n 2 + 2 1 + ⋯ + n 2 + n 1 ) y n = ( 1 n 2 + n + 1 n 2 + n + ⋯ + 1 n 2 + n ) = n n 2 + n = 1 1 n + 1 y_n=(\frac{1}{\sqrt{n^2+n}}+\frac{1}{\sqrt{n^2+n}}+\cdots+\frac{1}{\sqrt{n^2+n}})=\frac{n}{\sqrt{n^2+n}}=\frac{1}{\sqrt{\frac{1}{n}+1}} y n = ( n 2 + n 1 + n 2 + n 1 + ⋯ + n 2 + n 1 ) = n 2 + n n = n 1 + 1 1 z n = ( 1 n 2 + 1 + 1 n 2 + 1 + ⋯ + 1 n 2 + 1 ) = n n 2 + 1 = 1 1 n 2 + 1 z_n=(\frac{1}{\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+1}}+\cdots+\frac{1}{\sqrt{n^2+1}})=\frac{n}{\sqrt{n^2+1}}=\frac{1}{\sqrt{\frac{1}{n^2}+1}} z n = ( n 2 + 1 1 + n 2 + 1 1 + ⋯ + n 2 + 1 1 ) = n 2 + 1 n = n 2 1 + 1 1 lim n → ∞ y n = 1 1 n + 1 = 1 \lim_{n\rightarrow\infty}{y_n}=\frac{1}{\sqrt{\frac{1}{n}+1}}=1 lim n → ∞ y n = n 1 + 1 1 = 1 lim n → ∞ z n = 1 1 n 2 + 1 = 1 \lim_{n\rightarrow\infty}{z_n}=\frac{1}{\sqrt{\frac{1}{n^2}+1}}=1 lim n → ∞ z n = n 2 1 + 1 1 = 1
函数 函数的极限x → ∞ x\to\infty x → ∞ f ( x ) f(x) f ( x ) ∣ x ∣ |x| ∣ x ∣ ∀ ε > 0 \forall \varepsilon>0 ∀ ε > 0 ∃ \exists ∃ X X X ∣ x ∣ > X |x|>X ∣ x ∣ > X ∣ f ( x ) − A ∣ < ε |f(x)-A|<\varepsilon ∣ f ( x ) − A ∣ < ε A A A f ( x ) f(x) f ( x ) x → ∞ x\to\infty x → ∞ lim n → ∞ f ( x ) = A \lim_{n\rightarrow\infty}f(x)=A lim n → ∞ f ( x ) = A
对于函数f ( x ) f(x) f ( x ) x 0 x_0 x 0 ∀ ε > 0 \forall \varepsilon >0 ∀ ε > 0 ∃ \exists ∃ δ \delta δ 0 < ∣ x − x 0 ∣ < δ 0<|x-x_0|<\delta 0 < ∣ x − x 0 ∣ < δ ∣ f ( x ) − A ∣ < ε |f(x)-A|<\varepsilon ∣ f ( x ) − A ∣ < ε A A A f ( x ) f(x) f ( x ) x → x 0 x \to x_0 x → x 0 lim x → x 0 f ( x ) = A \lim_{x \to x_0} f(x)=A lim x → x 0 f ( x ) = A
数列极限只有n → ∞ n \to \infty n → ∞ x → ∞ x \to \infty x → ∞ x → x 0 x \to x_0 x → x 0
数列极限可以称为收敛,而函数极限不提收敛的概念;
函数极限x → ∞ 可分为 x → − ∞ 和 x → + ∞ x \to \infty可分为x \to -\infty和x \to +\infty x → ∞ 可 分 为 x → − ∞ 和 x → + ∞
函数极限x → x 0 可分为 x → x 0 − 和 x → x 0 + x \to x_0可分为x \to x_0^-和x \to x_0^+ x → x 0 可 分 为 x → x 0 − 和 x → x 0 +
函数极限和数列极限都具有唯一性。
例:f ( x ) = 1 x f(x)=\frac{1}{x} f ( x ) = x 1 lim x → ∞ 1 x = 0 \lim_{x \to \infty} \frac{1}{x}=0 lim x → ∞ x 1 = 0 lim x → 0 1 x = ∞ \lim_{x \to 0} \frac{1}{x}=\infty lim x → 0 x 1 = ∞ f ( x ) = e x f(x)=e^x f ( x ) = e x lim x → ∞ e x = { lim x → + ∞ e x = + ∞ lim x → − ∞ e x = 0 → \lim_{x \to \infty}{e^x}=\begin{cases} \lim_{x \to +\infty} {e^x}=+\infty\\\\ \lim_{x \to -\infty}{e^x}=0\end{cases}\to lim x → ∞ e x = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ lim x → + ∞ e x = + ∞ lim x → − ∞ e x = 0 → lim x → 0 e x = { lim x → 0 + e x = 1 lim x → 0 − e x = 1 → 1 \lim_{x \to 0}{e^x}=\begin{cases} \lim_{x \to 0^+} {e^x}=1\\\\ \lim_{x \to 0^-}{e^x}=1\end{cases}\to1 lim x → 0 e x = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ lim x → 0 + e x = 1 lim x → 0 − e x = 1 → 1
lim x → − ∞ f ( x ) = lim x → + ∞ f ( x ) = A → lim x → ∞ f ( x ) = A \lim_{x \to -\infty}{f(x)=\lim_{x \to +\infty}{f(x)=A}}\to\lim_{x \to \infty}{f(x)=A} lim x → − ∞ f ( x ) = lim x → + ∞ f ( x ) = A → lim x → ∞ f ( x ) = A lim x → x 0 − f ( x ) = lim x → x 0 + f ( x ) = A → lim x → x 0 f ( x ) = A \lim_{x \to x_0^-}{f(x)=\lim_{x \to x_0^+}{f(x)=A}}\to \lim_{x \to x_0}{f(x)=A} lim x → x 0 − f ( x ) = lim x → x 0 + f ( x ) = A → lim x → x 0 f ( x ) = A
函数极限的四则运算 如果lim f ( x ) = A , lim g ( x ) = B \lim{f(x)=A},\lim{g(x)=B} lim f ( x ) = A , lim g ( x ) = B
lim [ f ( x ) ± g ( x ) ] = lim f ( x ) ± lim g ( x ) = A ± B \lim{\left [ f(x) \pm g(x) \right ] }=\lim{f(x)} \pm \lim{g(x)}=A \pm B lim [ f ( x ) ± g ( x ) ] = lim f ( x ) ± lim g ( x ) = A ± B lim [ f ( x ) ⋅ g ( x ) ] = lim f ( x ) ⋅ lim g ( x ) = A ⋅ B \lim{\left [ f(x) \cdot g(x) \right ] }=\lim{f(x)} \cdot \lim{g(x)}=A \cdot B lim [ f ( x ) ⋅ g ( x ) ] = lim f ( x ) ⋅ lim g ( x ) = A ⋅ B 若又B ≠ 0 ,则有 lim f ( x ) g ( x ) = lim f ( x ) lim g ( x ) = A B B \ne 0,则有\lim{\frac{f(x)}{g(x)}}=\frac{\lim{f(x)}}{\lim{g(x)}}=\frac{A}{B} B = 0 , 则 有 lim g ( x ) f ( x ) = l i m g ( x ) l i m f ( x ) = B A
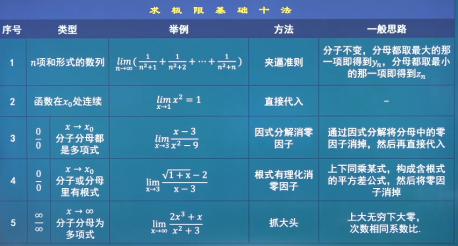
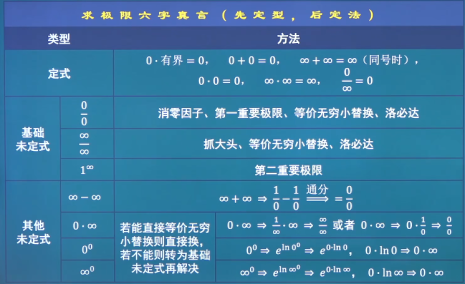
lim [ c ⋅ f ( x ) ] = c ⋅ lim f ( x ) = c ⋅ A ( c 为常数 ) \lim{\left [ c \cdot f(x) \right ] }=c \cdot \lim{f(x)}=c \cdot A(c为常数) lim [ c ⋅ f ( x ) ] = c ⋅ lim f ( x ) = c ⋅ A ( c 为 常 数 ) lim [ f ( x ) ] n = [ lim f ( x ) ] n = A n ( n 是正整数 ) \lim{\left [ f(x) \right ]^n }=\left [ \lim{f(x)} \right ]^n=A^n(n是正整数) lim [ f ( x ) ] n = [ lim f ( x ) ] n = A n ( n 是 正 整 数 ) x 0 、 x 0 + 、 x 0 − 、 ∞ 、 + ∞ 、 − ∞ x_0、x_0^+、x_0^-、\infty、+\infty、-\infty x 0 、 x 0 + 、 x 0 − 、 ∞ 、 + ∞ 、 − ∞ 复合函数极限运算法则 设函数y = f [ g ( x ) ] 是由函数 y = f ( u ) 与函数 u = g ( x ) y=f \left [ g(x) \right ]是由函数y=f(u)与函数u=g(x) y = f [ g ( x ) ] 是 由 函 数 y = f ( u ) 与 函 数 u = g ( x ) lim x → x 0 g ( x ) = u 0 ,且 lim u → u 0 f ( x ) = A \lim_{x \to x_0}{g(x)}=u_0,且\lim_{u \to u_0}{f(x)}=A lim x → x 0 g ( x ) = u 0 , 且 lim u → u 0 f ( x ) = A lim x → x 0 f [ g ( x ) ] = lim u → u 0 f ( x ) = A \lim_{x \to x_0}{f \left [ g(x) \right ] }=\lim_{u \to u_0}{f(x)}=A lim x → x 0 f [ g ( x ) ] = lim u → u 0 f ( x ) = A 因式分解消零因子法求极限* 例:lim x → 3 x − 3 x 2 − 9 \lim_{x \to 3}{\frac{x-3}{x^2-9}} lim x → 3 x 2 − 9 x − 3 x → 3 x \to 3 x → 3 3 − 3 9 − 9 = 0 0 \frac{3-3}{9-9}=\frac{0}{0} 9 − 9 3 − 3 = 0 0 ∵ 0 0 \because \frac{0}{0} ∵ 0 0 ∴ lim x → 3 x − 3 x 2 − 9 = lim x → 3 x − 3 ( x − 3 ) ( x + 3 ) = 1 x + 3 = 1 6 \therefore \lim_{x \to 3}{\frac{x-3}{x^2-9}}=\lim_{x \to 3}{\frac{x-3}{(x-3)(x+3)}}=\frac{1}{x+3}=\frac{1}{6} ∴ lim x → 3 x 2 − 9 x − 3 = lim x → 3 ( x − 3 ) ( x + 3 ) x − 3 = x + 3 1 = 6 1 x n − 1 = ( x − 1 ) ( 1 + x + x 2 + ⋯ + x n − 1 ) x^n-1=(x-1)(1+x+x^2+ \cdots +x^{n-1}) x n − 1 = ( x − 1 ) ( 1 + x + x 2 + ⋯ + x n − 1 ) a n − b n = ( a − b ) ( a n − 1 + a n − 2 b + ⋯ + a b n − 2 + b n − 1 ) a^n-b^n=(a-b)(a^{n-1}+a^{n-2}b+ \cdots +ab^{n-2}+b^{n-1}) a n − b n = ( a − b ) ( a n − 1 + a n − 2 b + ⋯ + a b n − 2 + b n − 1 ) 0 0 \frac{0}{0} 0 0 根式有理化消零因子法求极限* 例:求lim x → 3 1 − x − 2 x − 3 \lim_{x \to 3}{\frac{\sqrt{1-x}-2 }{x-3}} lim x → 3 x − 3 1 − x − 2 ∴ 分子分母同乘 1 − x + 2 \therefore分子分母同乘\sqrt{1-x}+2 ∴ 分 子 分 母 同 乘 1 − x + 2 lim x → 3 ( 1 − x − 2 ) ( 1 − x + 2 ) ( x − 3 ) ( 1 − x + 2 ) \lim_{x \to 3}{\frac{(\sqrt{1-x}-2)(\sqrt{1-x}+2) }{(x-3)(\sqrt{1-x}+2)}} lim x → 3 ( x − 3 ) ( 1 − x + 2 ) ( 1 − x − 2 ) ( 1 − x + 2 ) = lim x → 3 1 + x − 4 ( x − 3 ) ( 1 − x + 2 ) =\lim_{x \to 3}{\frac{1+x-4}{(x-3)(\sqrt{1-x}+2)}} = lim x → 3 ( x − 3 ) ( 1 − x + 2 ) 1 + x − 4 = lim x → 3 x − 3 ( x − 3 ) ( 1 − x + 2 ) =\lim_{x \to 3}{\frac{x-3}{(x-3)(\sqrt{1-x}+2)}} = lim x → 3 ( x − 3 ) ( 1 − x + 2 ) x − 3 = lim x → 3 1 1 − x + 2 =\lim_{x \to 3}{\frac{1}{\sqrt{1-x}+2}} = lim x → 3 1 − x + 2 1 = 1 4 =\frac{1}{4} = 4 1 抓大头法求极限* 例:求lim x → ∞ 2 x + 1 x 2 + 3 \lim_{x \to \infty} {\frac{2x+1}{x^2+3}} lim x → ∞ x 2 + 3 2 x + 1 x 2 x^2 x 2 = lim x → ∞ 2 x + 1 x 2 1 + 3 x 2 =\lim_{x \to \infty} {\frac{\frac{2}{x}+\frac{1}{x^2}}{1+\frac{3}{x^2} }} = lim x → ∞ 1 + x 2 3 x 2 + x 2 1 = 0 1 =\frac{0}{1} = 1 0 = 0 =0 = 0 lim x → ∞ 2 x 3 + x x 2 + 3 \lim_{x \to \infty} {\frac{2x^3+x}{x^2+3}} lim x → ∞ x 2 + 3 2 x 3 + x x 3 x^3 x 3 = lim x → ∞ 2 + 1 x 2 1 x + 3 x 3 =\lim_{x \to \infty} {\frac{2+\frac{1}{x^2}}{\frac{1}{x}+\frac{3}{x^3} }} = lim x → ∞ x 1 + x 3 3 2 + x 2 1 = 2 + 0 0 + 0 =\frac{2+0}{0+0} = 0 + 0 2 + 0 = ∞ =\infty = ∞ ∞ ∞ \frac{\infty}{\infty} ∞ ∞ ∞ \infty ∞ 0 0 0
课后习题
求极限lim x → 2 x 2 − x − 2 x 2 − 5 x + 6 \lim_{x \to 2}{\frac{x^2-x-2}{x^2-5x+6}} lim x → 2 x 2 − 5 x + 6 x 2 − x − 2 = lim x → 2 x 2 − x − 2 x 2 − 2 x − 3 x + 6 =\lim_{x \to 2}{\frac{x^2-x-2}{x^2-2x-3x+6}} = lim x → 2 x 2 − 2 x − 3 x + 6 x 2 − x − 2
= lim x → 2 x 2 + x − 2 x − 2 x 2 − 2 x − 3 x + 6 =\lim_{x \to 2}{\frac{x^2+x-2x-2}{x^2-2x-3x+6}} = lim x → 2 x 2 − 2 x − 3 x + 6 x 2 + x − 2 x − 2 = lim x → 2 x ( x + 1 ) − 2 ( x + 1 ) x ( x − 2 ) − 3 ( x − 2 ) =\lim_{x \to 2}{\frac{x(x+1)-2(x+1)}{x(x-2)-3(x-2)}} = lim x → 2 x ( x − 2 ) − 3 ( x − 2 ) x ( x + 1 ) − 2 ( x + 1 ) 分子提取公因式( x + 1 ) ,分母提取公因式 ( x − 2 ) (x+1),分母提取公因式(x-2) ( x + 1 ) , 分 母 提 取 公 因 式 ( x − 2 )
= lim x → 2 ( x + 1 ) ( x − 2 ) ( x − 2 ) ( x − 3 ) =\lim_{x \to 2}{\frac{(x+1)(x-2)}{(x-2)(x-3)}} = lim x → 2 ( x − 2 ) ( x − 3 ) ( x + 1 ) ( x − 2 ) = lim x → 2 x + 1 x − 3 =\lim_{x \to 2}{\frac{x+1}{x-3}} = lim x → 2 x − 3 x + 1 = lim x → 2 3 − 1 =\lim_{x \to 2}{\frac{3}{-1}} = lim x → 2 − 1 3 = − 3 =-3 = − 3 求极限lim x → 1 x 4 − 1 x 5 − 1 \lim_{x \to 1}{\frac{x^4-1}{x^5-1}} lim x → 1 x 5 − 1 x 4 − 1 = lim x → 1 ( x − 1 ) ( x 3 + x 2 + x + 1 ) ( x − 1 ) ( x 4 + x 3 + x 2 + x + 1 ) =\lim_{x \to 1} {\frac{(x-1)(x^3+x^2+x+1)}{(x-1)(x^4+x^3+x^2+x+1)} } = lim x → 1 ( x − 1 ) ( x 4 + x 3 + x 2 + x + 1 ) ( x − 1 ) ( x 3 + x 2 + x + 1 )
= 4 5 =\frac{4}{5} = 5 4 2.使用洛必达法则
= lim x → 1 d d x ( x 4 − 1 ) d d x ( x 5 − 1 ) =\lim_{x \to 1}{\frac{\frac{\mathrm{d} }{\mathrm{d} x} (x^4-1)}{\frac{\mathrm{d}}{\mathrm{d} x} (x^5-1)}} = lim x → 1 d x d ( x 5 − 1 ) d x d ( x 4 − 1 ) = lim x → 1 4 x 3 5 x 4 =\lim_{x \to 1}{\frac{4x^3}{5x^4}} = lim x → 1 5 x 4 4 x 3 = lim x → 1 4 5 x =\lim_{x \to 1}{\frac{4}{5x}} = lim x → 1 5 x 4 = 4 5 =\frac{4}{5} = 5 4 求极限lim x → 3 x + 2 − 5 x − 3 \lim_{x \to 3}{\frac{\sqrt{x+2}-\sqrt{5} }{x-3}} lim x → 3 x − 3 x + 2 − 5 x + 2 + 5 \sqrt{x+2}+\sqrt{5} x + 2 + 5
= x + 2 − 5 ( x − 3 ) ( x + 2 + 5 ) =\frac{x+2-5}{(x-3)(\sqrt{x+2}+\sqrt{5})} = ( x − 3 ) ( x + 2 + 5 ) x + 2 − 5 = x − 3 ( x − 3 ) ( x + 2 + 5 ) =\frac{x-3}{(x-3)(\sqrt{x+2}+\sqrt{5})} = ( x − 3 ) ( x + 2 + 5 ) x − 3 = 1 x + 2 + 5 =\frac{1}{\sqrt{x+2}+\sqrt{5}} = x + 2 + 5 1 = 5 10 =\frac{\sqrt{5}}{10} = 1 0 5 求极限lim x → ∞ x 2 − x − 2 x 2 − 5 x + 6 \lim_{x \to \infty}{\frac{x^2-x-2}{x^2-5x+6}} lim x → ∞ x 2 − 5 x + 6 x 2 − x − 2 ∴ = 1 \therefore =1 ∴ = 1
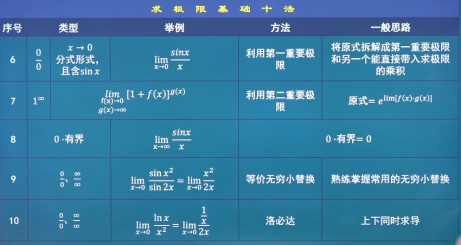
两个重要极限 第一重要极限 lim x → 0 sin x x = 1 \lim_{x \to 0} {\frac{\sin x}{x} }=1 lim x → 0 x s i n x = 1 函数夹逼准则:g ( x ) 、 f ( x ) 、 h ( x ) g(x)、f(x)、h(x) g ( x ) 、 f ( x ) 、 h ( x )
g ( x ) ≤ f ( x ) ≤ h ( x ) g(x)\le f(x) \le h(x) g ( x ) ≤ f ( x ) ≤ h ( x ) lim g ( x ) = A ,且 lim h ( x ) = A \lim{g(x)}=A,且\lim{h(x)}=A lim g ( x ) = A , 且 lim h ( x ) = A lim f ( x ) = A \lim{f(x)}=A lim f ( x ) = A lim x → 0 sin x x 2 \lim_{x \to 0} {\frac{\sin x}{x^2} } lim x → 0 x 2 s i n x = lim x → 0 sin x x × 1 x =\lim_{x \to 0} {\frac{\sin x}{x} \times \frac{1}{x} } = lim x → 0 x s i n x × x 1 = lim x → 0 sin x x × lim x → 0 1 x =\lim_{x \to 0} {\frac{\sin x}{x} } \times \lim_{x \to 0}{\frac{1}{x}} = lim x → 0 x s i n x × lim x → 0 x 1 = 1 × ∞ =1 \times \infty = 1 × ∞ = ∞ =\infty = ∞ lim x → 0 tan x x \lim_{x \to 0} {\frac{\tan x}{x} } lim x → 0 x t a n x = lim x → 0 sin x x × 1 cos x =\lim_{x \to 0} {\frac{\sin x}{x} \times \frac{1}{\cos x} } = lim x → 0 x s i n x × c o s x 1 = lim x → 0 sin x x × lim x → 0 1 cos x =\lim_{x \to 0} {\frac{\sin x}{x} } \times \lim_{x \to 0}{\frac{1}{\cos x}} = lim x → 0 x s i n x × lim x → 0 c o s x 1 = 1 × 1 =1 \times 1 = 1 × 1 = 1 =1 = 1 lim x → 0 arcsin x x \lim_{x \to 0} {\frac{\arcsin x}{x} } lim x → 0 x a r c s i n x x = sin t x=\sin t x = sin t arcsin x = t \arcsin x=t arcsin x = t = lim t → 0 t sin t =\lim_{t \to 0} {\frac{t}{\sin t}} = lim t → 0 s i n t t = 1 =1 = 1 0 0 极限趋近于 0 且含有 sin x \frac{0}{0}极限趋近于0且含有\sin x 0 0 极 限 趋 近 于 0 且 含 有 sin x
第二重要极限 lim x → ∞ ( 1 + 1 x ) 2 = e \lim_{x \to \infty} ({1+\frac{1}{x})^2 }=e lim x → ∞ ( 1 + x 1 ) 2 = e 例:求极限lim x → 0 ( 1 + x ) 1 x \lim_{x \to 0} ({1+x)^\frac{1}{x} } lim x → 0 ( 1 + x ) x 1 x = 1 t x=\frac{1}{t} x = t 1 = lim t → ∞ ( 1 + 1 t ) t =\lim_{t \to \infty} ({1+\frac{1}{t})^t } = lim t → ∞ ( 1 + t 1 ) t = e =e = e lim x → 0 ( 1 + x ) 1 x = e \lim_{x \to 0} ({1+x)^\frac{1}{x} }=e lim x → 0 ( 1 + x ) x 1 = e lim f ( x ) → 0 g ( x ) → ∞ [ 1 + f ( x ) ] g ( x ) = e lim [ f ( x ) ⋅ g ( x ) ] \lim_{f(x) \to 0 \ g(x) \to \infty }[1+f(x)]^{g(x)}=e^{\lim [f(x)\cdot g(x)]} lim f ( x ) → 0 g ( x ) → ∞ [ 1 + f ( x ) ] g ( x ) = e l i m [ f ( x ) ⋅ g ( x ) ] lim x → 0 ( 1 − 6 x ) 3 sin x \lim_{x \to 0} {(1-6x)^{\frac{3}{\sin x} }} lim x → 0 ( 1 − 6 x ) s i n x 3 = e lim x → 0 ( − 6 x ⋅ 3 sin x ) =e^{\lim_{x \to 0} {(-6x\cdot \frac{3}{\sin x}) }} = e l i m x → 0 ( − 6 x ⋅ s i n x 3 ) = e lim x → 0 ( − 18 x sin x ) =e^{\lim_{x \to 0} {(\frac{-18x}{\sin x}) }} = e l i m x → 0 ( s i n x − 1 8 x ) ∵ x sin x = 1 \because \frac{x}{\sin x}=1 ∵ s i n x x = 1 ∴ = e − 18 \therefore =e^{-18} ∴ = e − 1 8 1 ∞ 1^\infty 1 ∞
无穷小与无穷大 概念 如果 lim x → x 0 ∖ x → ∞ f ( x ) = 0 ,则称函数 f ( x ) 为当 x → x 0 或 x → ∞ 时无穷小; 如果\lim_{x \to x_0\setminus x \to \infty}{f(x)}=0,则称函数f(x)为当x \to x_0或x \to \infty时无穷小; 如 果 lim x → x 0 ∖ x → ∞ f ( x ) = 0 , 则 称 函 数 f ( x ) 为 当 x → x 0 或 x → ∞ 时 无 穷 小 ; 如果 lim x → x 0 ∖ x → ∞ f ( x ) = ∞ ,则称函数 f ( x ) 为当 x → x 0 或 x → ∞ 时无穷大; 如果\lim_{x \to x_0\setminus x \to \infty}{f(x)}=\infty,则称函数f(x)为当x \to x_0或x \to \infty时无穷大; 如 果 lim x → x 0 ∖ x → ∞ f ( x ) = ∞ , 则 称 函 数 f ( x ) 为 当 x → x 0 或 x → ∞ 时 无 穷 大 ; 无穷小与无穷大都是一个函数,不能与很小的数或者很大的数混为一谈,无穷小是一个趋近于0(可以为0)的过程。
无穷小的性质
在自变量的同一变化过程x → x 0 x \to x_0 x → x 0 x → ∞ x \to \infty x → ∞ f ( x ) f(x) f ( x ) A A A f ( x ) = A + α f(x)=A+\alpha f ( x ) = A + α α \alpha α
1 无穷小 = 无穷大 \frac{1}{无穷小}=无穷大 无 穷 小 1 = 无 穷 大 1 无穷大 = 无穷小 \frac{1}{无穷大}=无穷小 无 穷 大 1 = 无 穷 小 有限个无穷小的和是无穷小。
有界函数与无穷小的乘积是无穷小。lim x → ∞ sin x x = lim x → ∞ sin x ⋅ lim x → ∞ 1 x = 0 \lim_{x \to \infty}{\frac{\sin x}{x} }= \lim_{x \to \infty} {\sin x}\cdot \lim_{x \to \infty} {\frac{1}{x} } =0 lim x → ∞ x s i n x = lim x → ∞ sin x ⋅ lim x → ∞ x 1 = 0
lim x → 0 sin x x = 1 \lim_{x \to 0} {\frac{\sin x}{x} }=1 lim x → 0 x s i n x = 1 lim x → ∞ sin x x = 0 \lim_{x \to \infty } {\frac{\sin x}{x} }=0 lim x → ∞ x s i n x = 0 lim x → 0 x ⋅ sin 1 x = 0 \lim_{x \to 0 } {x \cdot \sin \frac{1}{x} }=0 lim x → 0 x ⋅ sin x 1 = 0 lim x → ∞ x ⋅ sin 1 x = 1 \lim_{x \to \infty } {x \cdot \sin \frac{1}{x} }=1 lim x → ∞ x ⋅ sin x 1 = 1 lim x → 0 1 x ⋅ sin 1 x = 无极限 \lim_{x \to 0 } {\frac{1}{x} \cdot \sin \frac{1}{x} }=无极限 lim x → 0 x 1 ⋅ sin x 1 = 无 极 限 ∞ \infty ∞ lim x → ∞ 1 x ⋅ sin 1 x = 0 \lim_{x \to \infty } {\frac{1}{x} \cdot \sin \frac{1}{x} }=0 lim x → ∞ x 1 ⋅ sin x 1 = 0
常数与无穷小的乘积是无穷小;
有限个无穷小的乘积是无穷小。0 ⋅ 有界 = 0 0 \cdot 有界 = 0 0 ⋅ 有 界 = 0 无穷小的比较 定义:设α \alpha α β \beta β β ≠ 0 \beta \ne 0 β = 0 lim α β = 0 \lim \frac{\alpha }{\beta } =0 lim β α = 0 ⇒ \Rightarrow ⇒ α \alpha α β \beta β α = o ( β ) \alpha=o(\beta ) α = o ( β ) lim α β = ∞ \lim \frac{\alpha }{\beta } =\infty lim β α = ∞ ⇒ \Rightarrow ⇒ α \alpha α β \beta β lim α β = c ≠ 0 \lim \frac{\alpha }{\beta } =c \ne 0 lim β α = c = 0 ⇒ \Rightarrow ⇒ α \alpha α β \beta β lim α β k = c ≠ 0 \lim \frac{\alpha }{\beta ^k} =c \ne 0 lim β k α = c = 0 ⇒ \Rightarrow ⇒ α \alpha α β \beta β k k k ( k > 0 ) (k>0 ) ( k > 0 ) lim α β = 1 \lim \frac{\alpha }{\beta } =1 lim β α = 1 ⇒ \Rightarrow ⇒ α \alpha α β \beta β α ∼ β \alpha \sim \beta α ∼ β
一般为分子是分母的~阶无穷小;
越高阶趋近于0的速度越快;
c可以是正数可以为负数,k可以是整数也可以是分数。
等价无穷小的性质
自反性:α ∼ α \alpha \sim \alpha α ∼ α
对称性:若α ∼ β \alpha \sim \beta α ∼ β β ∼ α \beta \sim \alpha β ∼ α
传递性:若α ∼ β \alpha \sim \beta α ∼ β β ∼ γ \beta \sim \gamma β ∼ γ α ∼ γ \alpha \sim \gamma α ∼ γ
可替换性:若α ∼ γ \alpha \sim \gamma α ∼ γ β ∼ θ \beta \sim \theta β ∼ θ lim α β = lim γ θ \lim \frac{\alpha }{\beta } =\lim \frac{\gamma }{\theta} lim β α = lim θ γ 0 0 \frac{0}{0} 0 0 ∞ ∞ \frac{\infty}{\infty} ∞ ∞ 0 ⋅ ∞ 0 \cdot \infty 0 ⋅ ∞
常用的等价无穷小替换* 当 x ⟶ 0 x\longrightarrow 0 x ⟶ 0
x ∼ sin x ∼ tan x ∼ arcsin x ∼ arctan x x\sim \sin x\sim \tan x\sim \arcsin x\sim \arctan x x ∼ sin x ∼ tan x ∼ arcsin x ∼ arctan x 1 − cos x ∼ 1 2 x 2 1-\cos x\sim \frac{1}{2} x^2 1 − cos x ∼ 2 1 x 2 l n ( 1 + x ) x ∼ x ln(1+x)x\sim x l n ( 1 + x ) x ∼ x e x − 1 ∼ x e^x-1 \sim x e x − 1 ∼ x ( 1 + x ) μ − 1 ∼ μ ⋅ x (1+x)^\mu-1 \sim \mu \cdot x ( 1 + x ) μ − 1 ∼ μ ⋅ x 1 + x n − 1 ∼ 1 n ⋅ x \sqrt[n]{1+x}-1 \sim \frac{1}{n} \cdot x n 1 + x − 1 ∼ n 1 ⋅ x □ \Box □ cos 2 α = cos 2 α − s i n 2 α = 2 cos 2 α − 1 = 1 − 2 sin 2 α \cos 2 \alpha =\cos ^2\alpha - \ sin ^2 \alpha = 2\cos ^2 \alpha -1 = 1-2\sin ^2 \alpha cos 2 α = cos 2 α − s i n 2 α = 2 cos 2 α − 1 = 1 − 2 sin 2 α 利用等价无穷小替换求极限 例:求极限lim x → 0 l n cos x x tan [ sin ( sin x ) ] \lim_{x \to 0} \frac{ln \cos x}{x \tan [\sin (\sin x)]} lim x → 0 x t a n [ s i n ( s i n x ) ] l n c o s x lim x → 0 1 2 x 2 x 2 = − 1 2 \lim_{x \to 0 }{\frac{\frac{1}{2}x^2}{x^2}}=-\frac{1}{2} lim x → 0 x 2 2 1 x 2 = − 2 1 l n cos x = l n ( cos x − 1 + 1 ) ∼ − 1 2 x 2 ln \cos x = ln(\cos x -1 +1) \sim - \frac{1}{2}x^2 l n cos x = l n ( cos x − 1 + 1 ) ∼ − 2 1 x 2 sin x ∼ x ∼ tan x = x 2 \sin x \sim x \sim \tan x =x^2 sin x ∼ x ∼ tan x = x 2 总结+习题 lim x → ∞ ( sin 3 x + 1 ) 2 x \lim_{x \to \infty} (\sin \frac{3}{x} +1)^{2x} lim x → ∞ ( sin x 3 + 1 ) 2 x = e lim x → ∞ ( sin 3 x ⋅ 2 x ) =e^{\lim_{x \to \infty} (\sin \frac{3}{x} \cdot 2x)} = e l i m x → ∞ ( s i n x 3 ⋅ 2 x ) sin 3 x ∼ 3 x \sin \frac{3}{x} \sim \frac{3}{x} sin x 3 ∼ x 3 = e lim x → ∞ ( 3 x ⋅ 2 x ) =e^{\lim_{x \to \infty} (\frac{3}{x} \cdot 2x)} = e l i m x → ∞ ( x 3 ⋅ 2 x ) = e 6 =e^6 = e 6 lim x → ∞ ( 3 x + 1 3 x − 1 ) 2 x + 3 \lim_{x \to \infty} (\frac{3x+1}{3x-1} )^{2x+3} lim x → ∞ ( 3 x − 1 3 x + 1 ) 2 x + 3 3 x + 1 3 x − 1 = 3 x − 1 + 2 3 x − 1 = 1 + 2 3 x − 1 \frac{3x+1}{3x-1}=\frac{3x-1+2}{3x-1}=1+\frac{2}{3x-1} 3 x − 1 3 x + 1 = 3 x − 1 3 x − 1 + 2 = 1 + 3 x − 1 2 = e lim x → ∞ [ 2 3 x − 1 ⋅ ( 2 x + 3 ) ] =e^{\lim_{x \to \infty} [\frac{2}{3x-1} \cdot (2x+3)]} = e l i m x → ∞ [ 3 x − 1 2 ⋅ ( 2 x + 3 ) ] = e lim x → ∞ ( 4 x + 6 3 x − 1 ) =e^{\lim_{x \to \infty} (\frac{4x+6}{3x-1})} = e l i m x → ∞ ( 3 x − 1 4 x + 6 ) = e 4 3 =e^{\frac{4}{3}} = e 3 4 lim x → ∞ ( x sin 1 x + 1 x sin x ) \lim_{x \to \infty} (x \sin \frac{1}{x}+\frac{1}{x} \sin x ) lim x → ∞ ( x sin x 1 + x 1 sin x ) = lim x → ∞ x ⋅ sin 1 x + lim x → ∞ 1 x sin x =\lim_{x \to \infty} x \cdot \sin \frac{1}{x}+\lim_{x \to \infty} \frac{1}{x}\sin x = lim x → ∞ x ⋅ sin x 1 + lim x → ∞ x 1 sin x = 1 + 0 = 1 =1+0=1 = 1 + 0 = 1 lim x → ∞ ( x − 1 2 x 2 + 5 + a x + b ) = 3 \lim_{x \to \infty} (\frac{x-1}{2x^2+5}+ax+b )=3 lim x → ∞ ( 2 x 2 + 5 x − 1 + a x + b ) = 3 = lim x → ∞ x − 1 2 x 2 + 5 + lim x → ∞ a x + lim x → ∞ b = 3 =\lim_{x \to \infty} \frac{x-1}{2x^2+5}+\lim_{x \to \infty} ax+\lim_{x \to \infty} b=3 = lim x → ∞ 2 x 2 + 5 x − 1 + lim x → ∞ a x + lim x → ∞ b = 3 = 0 + { a ≠ 0 ⇒ ∞ a = 0 ⇒ 0 + b = 3 =0+\left\{\begin{matrix}a\ne 0\Rightarrow \infty
\\
a=0\Rightarrow 0
\end{matrix}\right.+b=3 = 0 + { a = 0 ⇒ ∞ a = 0 ⇒ 0 + b = 3 ⇒ a = 0 \Rightarrow a=0 ⇒ a = 0 ∴ b = 3 \therefore b=3 ∴ b = 3 lim x → ∞ ( 2 x 2 + 5 x − 1 + a x + b ) = 3 \lim_{x \to \infty} (\frac{2x^2+5}{x-1}+ax+b )=3 lim x → ∞ ( x − 1 2 x 2 + 5 + a x + b ) = 3 = lim x → ∞ 2 x 2 + 5 + a x 2 − a x x − 1 + b = 3 =\lim_{x \to \infty} \frac{2x^2+5+ax^2-ax}{x-1}+b=3 = lim x → ∞ x − 1 2 x 2 + 5 + a x 2 − a x + b = 3 x 2 x^2 x 2 a = − 2 a=-2 a = − 2 = lim x → ∞ 2 x + 5 x − 1 + b = 3 =\lim_{x \to \infty}\frac{2x+5}{x-1}+b=3 = lim x → ∞ x − 1 2 x + 5 + b = 3 = 2 + b = 3 =2+b=3 = 2 + b = 3 ∴ b = 1 \therefore b=1 ∴ b = 1 lim x → 1 f ( x ) \lim_{x \to 1}f(x) lim x → 1 f ( x ) f ( x ) = 2 x 3 + 3 lim x → 1 f ( x ) f(x)=2x^3+3 \lim_{x\to 1}f(x) f ( x ) = 2 x 3 + 3 lim x → 1 f ( x ) f ( x ) f(x) f ( x ) lim x → 1 f ( x ) = A \lim_{x \to 1}f(x)=A lim x → 1 f ( x ) = A lim x → 1 f ( x ) = lim x → 1 2 x 3 + 3 A \lim_{x \to 1}f(x)=\lim_{x\to 1}2x^3+3A lim x → 1 f ( x ) = lim x → 1 2 x 3 + 3 A ∵ lim x → 1 f ( x ) = A \because \lim_{x\to 1}f(x)=A ∵ lim x → 1 f ( x ) = A ∴ A = 2 + 3 A \therefore A=2+3A ∴ A = 2 + 3 A ∴ A = − 1 \therefore A=-1 ∴ A = − 1 ∴ f ( x ) = 2 x 3 − 3 \therefore f(x)=2x^3-3 ∴ f ( x ) = 2 x 3 − 3 lim x → 0 l n ( 1 + f ( x ) x ) e 2 x − 1 = 5 \lim_{x \to 0}\frac{ln(1+\frac{f(x)}{x})}{e^{2x}-1}=5 lim x → 0 e 2 x − 1 l n ( 1 + x f ( x ) ) = 5 x → 0 x \to 0 x → 0 f ( x ) x \frac{f(x)}{x} x f ( x ) lim x → 0 f ( x ) x 2 \lim_{x \to 0} \frac{f(x)}{x^2} lim x → 0 x 2 f ( x ) = lim x → 0 f ( x ) x 2 x =\lim_{x\to 0}\frac{\frac{f(x)}{x}}{2x} = lim x → 0 2 x x f ( x ) = lim x → 0 f ( x ) 2 x 2 =\lim_{x\to 0}\frac{f(x)}{2x^2} = lim x → 0 2 x 2 f ( x ) ∵ lim x → 0 f ( x ) 2 x 2 = 5 \because \lim_{x\to 0}\frac{f(x)}{2x^2}=5 ∵ lim x → 0 2 x 2 f ( x ) = 5 ∴ f ( x ) ∼ 10 x 2 \therefore f(x)\sim10x^2 ∴ f ( x ) ∼ 1 0 x 2 ∴ lim x → 0 f ( x ) x 2 = 10 x 2 x 2 = 10 \therefore\lim_{x \to 0} \frac{f(x)}{x^2}=\frac{10x^2}{x^2}=10 ∴ lim x → 0 x 2 f ( x ) = x 2 1 0 x 2 = 1 0
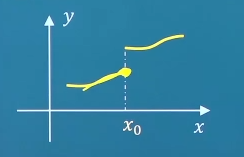
连续 函数的连续性 连续的概念 设函数y = f ( x ) y=f(x) y = f ( x ) x 0 x_0 x 0 lim x → x 0 f ( x ) = f ( x 0 ) \lim_{x \to x_0}f(x)=f(x_0) lim x → x 0 f ( x ) = f ( x 0 ) f ( x ) f(x) f ( x ) x 0 x_0 x 0 lim Δ x → 0 Δ y = lim Δ x → 0 [ f ( x 0 + Δ x ) − f ( x 0 ) ] = 0 \lim_{\Delta x \to 0} \Delta y=\lim_{\Delta x \to 0} [f(x_0+\Delta x)-f(x_0)]=0 lim Δ x → 0 Δ y = lim Δ x → 0 [ f ( x 0 + Δ x ) − f ( x 0 ) ] = 0 f ( x ) f(x) f ( x ) x 0 x_0 x 0
左连续的概念: lim x → x 0 − f ( x ) \lim_{x \to x_0^-}f(x) lim x → x 0 − f ( x ) f ( x 0 ) f(x_0) f ( x 0 ) f ( x ) f(x) f ( x ) x 0 x_0 x 0 f ( x 0 − ) f(x_0^-) f ( x 0 − ) 右连续的概念: lim x → x 0 + f ( x ) \lim_{x \to x_0^+}f(x) lim x → x 0 + f ( x ) f ( x 0 ) f(x_0) f ( x 0 ) f ( x ) f(x) f ( x ) x 0 x_0 x 0 f ( x 0 + ) f(x_0^+) f ( x 0 + ) 函数f ( x ) f(x) f ( x ) x 0 x_0 x 0 f ( x 0 − ) = f ( x 0 + ) = f ( x 0 ) f(x_0^-)=f(x_0^+)=f(x_0) f ( x 0 − ) = f ( x 0 + ) = f ( x 0 )
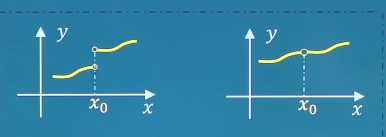
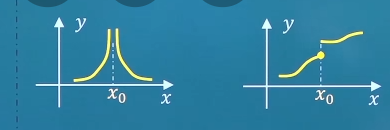
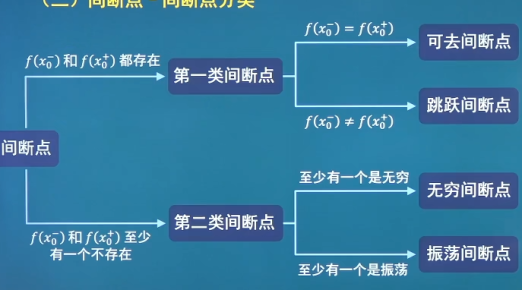
间断点 如果函数f ( x ) f(x) f ( x ) x 0 x_0 x 0 x 0 x_0 x 0 f ( x ) f(x) f ( x )
在x = x 0 x=x_0 x = x 0
虽有定义,但lim x → x 0 f ( x ) \lim_{x \to x_0}f(x) lim x → x 0 f ( x )
虽有定义,且lim x → x 0 f ( x ) \lim_{x \to x_0}f(x) lim x → x 0 f ( x ) lim x → x 0 f ( x ) ≠ f ( x 0 ) \lim_{x \to x_0}f(x) \ne f(x_0) lim x → x 0 f ( x ) = f ( x 0 ) 间断点-间断点分类 如果x 0 x_0 x 0 f ( x ) f(x) f ( x ) f ( x 0 − ) f(x_0^-) f ( x 0 − ) f ( x 0 + ) f(x_0^+) f ( x 0 + ) x 0 x_0 x 0 f ( x ) f(x) f ( x )
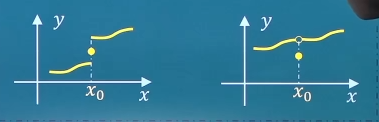
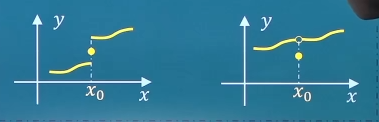
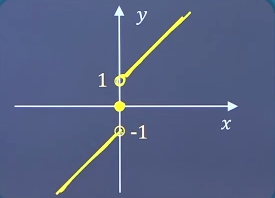
第一类:可去间断点f ( x 0 − ) = f ( x 0 + ) f(x_0^-)=f(x_0^+) f ( x 0 − ) = f ( x 0 + ) x 0 x_0 x 0 f ( x ) f(x) f ( x ) y = x 2 − 1 x − 1 , x = 1 y=\frac{x^2-1}{x-1},x=1 y = x − 1 x 2 − 1 , x = 1 y = { x , x ≠ 1 1 2 , x = 1 , x = 1 y=\left\{\begin{matrix}x,x\ne 1 \\ \frac{1}{2},x=1 \end{matrix}\right.,x=1 y = { x , x = 1 2 1 , x = 1 , x = 1
第一类:跳跃间断点f ( x 0 − ) f(x_0^-) f ( x 0 − ) f ( x 0 + ) f(x_0^+) f ( x 0 + ) f ( x 0 − ) ≠ f ( x 0 + ) f(x_0^-)\ne f(x_0^+) f ( x 0 − ) = f ( x 0 + ) x 0 x_0 x 0 f ( x ) f(x) f ( x ) y = { x − 1 , x < 0 0 , x = 0 x + 1 , x > 0 , x = 0 y=\left\{\begin{matrix}x-1,x<0 \\0,x=0 \\x+1,x>0 \end{matrix}\right.,x=0 y = ⎩ ⎪ ⎨ ⎪ ⎧ x − 1 , x < 0 0 , x = 0 x + 1 , x > 0 , x = 0
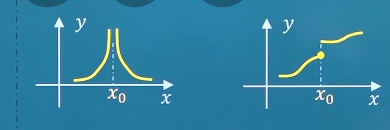
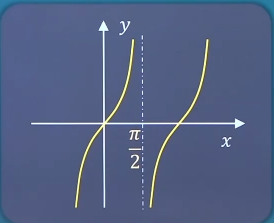
第二类:无穷间断点f ( x 0 − ) f(x_0^-) f ( x 0 − ) f ( x 0 + ) f(x_0^+) f ( x 0 + ) ∞ \infty ∞ x 0 x_0 x 0 f ( x ) f(x) f ( x ) y = tan x , x = π 2 y=\tan x,x=\frac{\pi}{2} y = tan x , x = 2 π
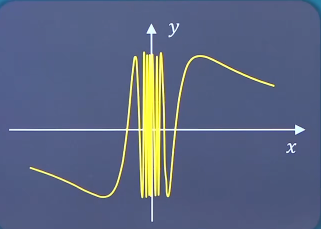
第二类:振荡间断点f ( x 0 − ) f(x_0^-) f ( x 0 − ) f ( x 0 + ) f(x_0^+) f ( x 0 + ) x 0 x_0 x 0 f ( x ) f(x) f ( x ) y = sin 1 x , x = 0 y=\sin \frac{1}{x},x=0 y = sin x 1 , x = 0
初等函数的连续性
一切初等函数在其定义区间内都是连续的。
若两个函数都连续,则它们的和、差、积、商都连续。
若两个函数都连续,则由它们构成的复合函数也连续。
若一个函数连续且有反函数,则它的反函数也连续。
闭区间上连续函数的性质
【有界性与最大值最小值定理】在闭区间上连续的函数在该区间上有界,且一定能取得它的最大值和最小值。
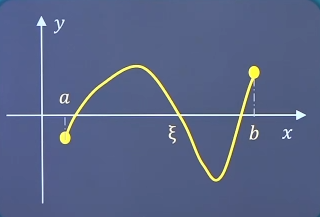
【零点定理】若函数f ( x ) f(x) f ( x ) [ a , b ] [a,b] [ a , b ] f ( a ) f(a) f ( a ) f ( b ) f(b) f ( b ) f ( a ) ⋅ f ( b ) < 0 f(a)\cdot f(b)<0 f ( a ) ⋅ f ( b ) < 0 ξ ∈ ( a , b ) \xi \in (a,b) ξ ∈ ( a , b ) f ( ξ ) = 0 f(\xi)=0 f ( ξ ) = 0
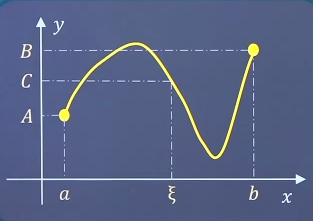
【介值定理】设函数f ( x ) f(x) f ( x ) [ a , b ] [a,b] [ a , b ] f ( a ) = A f(a)=A f ( a ) = A f ( b ) = B f(b)=B f ( b ) = B A A A B B B C C C ( a , b ) (a,b) ( a , b ) ξ \xi ξ f ( ξ ) = C f(\xi)=C f ( ξ ) = C 连续考点 判断函数在某点的连续性 例题:判断函数f ( x ) = { x + 1 2 , x < 0 1 2 , x = 0 l n ( 1 + x ) 2 x , x > 0 f(x)=\left\{\begin{matrix}x+\frac{1}{2},x<0 \\ \frac{1}{2},x=0 \\ \frac{ln(1+x)}{2x},x>0 \end{matrix}\right. f ( x ) = ⎩ ⎪ ⎨ ⎪ ⎧ x + 2 1 , x < 0 2 1 , x = 0 2 x l n ( 1 + x ) , x > 0 x = 0 x=0 x = 0 f ( x ) f(x) f ( x ) x 0 x_0 x 0 f ( x 0 − ) = f ( x 0 + ) = f ( x 0 ) f(x_0^-)=f(x_0^+)=f(x_0) f ( x 0 − ) = f ( x 0 + ) = f ( x 0 ) f ( 0 − ) = lim x → 0 − x + 1 2 = 1 2 f(0^-)=\lim_{x \to 0^-}x+\frac{1}{2}=\frac{1}{2} f ( 0 − ) = lim x → 0 − x + 2 1 = 2 1 f ( 0 + ) = lim x → 0 + l n ( 1 + x ) 2 x = lim x → 0 + x 2 x = 1 2 f(0^+)=\lim_{x \to 0^+}\frac{ln(1+x)}{2x}=\lim_{x \to 0^+}\frac{x}{2x}=\frac{1}{2} f ( 0 + ) = lim x → 0 + 2 x l n ( 1 + x ) = lim x → 0 + 2 x x = 2 1 ∴ f ( 0 − ) = f ( 0 + ) = f ( 0 ) = 1 2 \therefore f(0^-)=f(0^+)=f(0)=\frac{1}{2} ∴ f ( 0 − ) = f ( 0 + ) = f ( 0 ) = 2 1 ∴ \therefore ∴
已知函数在某点连续求系数 例题:设函数f ( x ) = { x sin 1 x , x < 0 a + x x 2 , x ≥ 0 f(x)=\left\{\begin{matrix}x \sin \frac{1}{x},x<0 \\a+xx^2,x\ge 0\end{matrix}\right. f ( x ) = { x sin x 1 , x < 0 a + x x 2 , x ≥ 0 x = 0 x=0 x = 0 a = a= a = _0 f ( x 0 − ) = f ( x 0 + ) = f ( x 0 ) f(x_0^-)=f(x_0^+)=f(x_0) f ( x 0 − ) = f ( x 0 + ) = f ( x 0 ) f ( 0 ) = a + 0 2 = a f(0)=a+0^2=a f ( 0 ) = a + 0 2 = a f ( 0 − ) = lim x → 0 − x ⋅ sin 1 x f(0^-)=\lim_{x \to 0^-}x \cdot \sin \frac{1}{x} f ( 0 − ) = lim x → 0 − x ⋅ sin x 1 0 − 0^- 0 − sin 1 0 − : 1 0 − = − ∞ \sin \frac{1}{0^-}:\frac{1}{0^-}=-\infty sin 0 − 1 : 0 − 1 = − ∞ 0 − ⋅ 有界 = 0 0^- \cdot 有界 = 0 0 − ⋅ 有 界 = 0 ∴ a = 0 \therefore a=0 ∴ a = 0 1 0 − = − ∞ \frac{1}{0^-}=-\infty 0 − 1 = − ∞ 1 0 + = + ∞ \frac{1}{0^+}=+\infty 0 + 1 = + ∞
判断间断点个数 例题:函数f ( x ) = sin x x + 1 x − 1 e 1 x f(x)=\frac{\sin x}{x}+\frac{1}{x-1}e^{\frac{1}{x} } f ( x ) = x s i n x + x − 1 1 e x 1 x x x sin x x \frac{\sin x}{x} x s i n x 1 x − 1 \frac{1}{x-1} x − 1 1 1 x \frac{1}{x} x 1 x ≠ 0 x\ne0 x = 0 x − 1 ≠ 0 x-1\ne0 x − 1 = 0 ∴ x ≠ 0 或 x ≠ 1 \therefore x\ne0或x\ne1 ∴ x = 0 或 x = 1
判断间断点类型 例题:设函数f ( x ) = { cos x + 1 x , x ≠ 0 0 , x = 0 f(x)=\left\{\begin{matrix}\frac{\cos x+1}{x},x\ne 0 \\0,x=0\end{matrix}\right. f ( x ) = { x c o s x + 1 , x = 0 0 , x = 0 x = 0 x=0 x = 0 f ( 0 − ) = cos x x = 1 + 1 0 − = − ∞ f(0^-)=\frac{\cos x}{x}=\frac{1+1}{0^-}=-\infty f ( 0 − ) = x c o s x = 0 − 1 + 1 = − ∞ f ( 0 + ) = + ∞ f(0^+)=+\infty f ( 0 + ) = + ∞ ∴ \therefore ∴
已知间断类型求系数 例题:已知点x = 1 x=1 x = 1 f ( x ) = x − a x 2 − 4 x + 3 f(x)=\frac{x-a}{x^2-4x+3} f ( x ) = x 2 − 4 x + 3 x − a a = a= a = f ( x 0 − ) = f ( x 0 + ) f(x_0^-)=f(x_0^+) f ( x 0 − ) = f ( x 0 + ) lim x → 1 x − a x 2 − 4 x + 3 \lim_{x \to 1}\frac{x-a}{x^2-4x+3} lim x → 1 x 2 − 4 x + 3 x − a □ 0 = A \frac{\Box }{0} =A 0 □ = A 0 0 = A \frac{0}{0}=A 0 0 = A ∴ x − a = 0 ,即 1 − a = 0 , a = 1 \therefore x-a=0,即1-a=0,a=1 ∴ x − a = 0 , 即 1 − a = 0 , a = 1
证明方程在某区间内至少有一个实根——零点定理 x 3 + 3 x 2 = 1 x^3+3x^2=1 x 3 + 3 x 2 = 1 ( 0 , 1 ) (0,1) ( 0 , 1 ) x 3 + 3 x 2 − 1 = 0 x^3+3x^2-1=0 x 3 + 3 x 2 − 1 = 0 f ( x ) = x 3 + 3 x 2 − 1 f(x)=x^3+3x^2-1 f ( x ) = x 3 + 3 x 2 − 1 f ( x ) f(x) f ( x ) [ 0 , 1 ] [0,1] [ 0 , 1 ] f ( 0 ) = 0 3 + 3 ⋅ 0 2 − 1 = − 1 f(0)=0^3+3 \cdot 0^2-1=-1 f ( 0 ) = 0 3 + 3 ⋅ 0 2 − 1 = − 1 f ( 1 ) = 1 3 + 3 ⋅ 1 2 − 1 = 3 f(1)=1^3+3 \cdot 1^2 -1=3 f ( 1 ) = 1 3 + 3 ⋅ 1 2 − 1 = 3 ∵ f ( 0 ) ⋅ f ( 1 ) < 0 \because f(0)\cdot f(1)<0 ∵ f ( 0 ) ⋅ f ( 1 ) < 0 ∴ \therefore ∴ ξ ∈ ( 0 , 1 ) \xi \in (0,1) ξ ∈ ( 0 , 1 ) f ( ξ ) = 0 f(\xi)=0 f ( ξ ) = 0 x 3 + 3 x 2 = 1 x^3+3x^2=1 x 3 + 3 x 2 = 1 ( 0 , 1 ) (0,1) ( 0 , 1 ) e x = 3 x e^x=3x e x = 3 x ( 0 , 1 ) (0,1) ( 0 , 1 ) e x − 3 x = 0 e^x-3x=0 e x − 3 x = 0 f ( x ) = e x − 3 x f(x)=e^x-3x f ( x ) = e x − 3 x f ( x ) f(x) f ( x ) [ 0 , 1 ] [0,1] [ 0 , 1 ] f ( 0 ) = e 0 + 3 ⋅ 0 = 1 f(0)=e^0+3 \cdot 0=1 f ( 0 ) = e 0 + 3 ⋅ 0 = 1 f ( 1 ) = e − 3 < 0 f(1)=e-3<0 f ( 1 ) = e − 3 < 0 e ≈ 2.718 e \approx 2.718 e ≈ 2 . 7 1 8 ∵ f ( 0 ) ⋅ f ( 1 ) < 0 \because f(0)\cdot f(1)<0 ∵ f ( 0 ) ⋅ f ( 1 ) < 0 ∴ \therefore ∴ ξ ∈ ( 0 , 1 ) \xi \in (0,1) ξ ∈ ( 0 , 1 ) f ( ξ ) = 0 f(\xi)=0 f ( ξ ) = 0 e x = 3 x e^x=3x e x = 3 x ( 0 , 1 ) (0,1) ( 0 , 1 )
课后习题