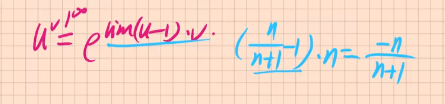常微分方程和无穷级数 常微分方程 一、基本概念
含有y y y
微分方程的阶:指微分方程中最高阶导数;
微分方程的解:满足微分方程的函数y y y
微分方程解的类型:a. 含有独立的任意常数C;b. 且C的个数于阶数相同; )不含C )
阶数识别 y ( n ) y^{(n)} y ( n ) 叫n阶导;
d y d x = y ′ , d 2 y d x 2 y ′ ′ \frac{dy}{dx}=y',\frac{d^2y}{dx^2}y'' d x d y = y ′ , d x 2 d 2 y y ′ ′ 阶数取决于整个方程中导数的最高阶导,而不是变量的次数。不是 幂函数;( y ′ ′ ) 5 + 2 ( y ′ ) 3 + x y 6 = 0 (y'')^5+2(y')^3+xy^6=0 ( y ′ ′ ) 5 + 2 ( y ′ ) 3 + x y 6 = 0 ( y ′ ) 3 + y ′ ′ ⋅ y 4 − 3 x y = 0 (y')^3+y''\cdot y^4-3xy=0 ( y ′ ) 3 + y ′ ′ ⋅ y 4 − 3 x y = 0 ( d 2 y d x 2 ) 4 + y ⋅ d y d x = 0 (\frac{d^2y}{dx^2})^4+y\cdot \frac{dy}{dx}=0 ( d x 2 d 2 y ) 4 + y ⋅ d x d y = 0 ( y ′ ) 3 + y ′ ′ ⋅ y ( 4 ) − 3 x y = 0 (y')^3+y''\cdot y^{(4)}-3xy=0 ( y ′ ) 3 + y ′ ′ ⋅ y ( 4 ) − 3 x y = 0
线性微分方程识别 称方程中的未知函数y y y y ′ , y ′ ′ y',y'' y ′ , y ′ ′ x y ′ ′ + 2 y ′ + x 2 y = 0 xy''+2y'+x^2y=0 x y ′ ′ + 2 y ′ + x 2 y = 0 y ′ ′ + ( ln x ) ⋅ y ′ + cos x y = 0 y''+(\ln x)\cdot y'+\cos xy=0 y ′ ′ + ( ln x ) ⋅ y ′ + cos x y = 0 y ′ ′ + 2 y ′ + y 2 = e x y''+2y'+y^2=e^x y ′ ′ + 2 y ′ + y 2 = e x y ′ − x y + 1 = ln x y'-xy+1=\ln x y ′ − x y + 1 = ln x ( y ′ ′ ) 2 − y ′ = 3 x + 7 (y'')^2-y'=3x+7 ( y ′ ′ ) 2 − y ′ = 3 x + 7
齐次微分方程识别 y y y 及其相关导数
= Q ( x ) =Q(x) = Q ( x ) 全为x的函数(自由项)
→ { ( x ) = 0 ,齐次 ( x ) ≠ 0 ,非齐次 \rightarrow \left\{\begin{matrix}(x)=0,齐次\\(x)\ne 0 , 非齐次\end{matrix}\right. → { ( x ) = 0 , 齐 次 ( x ) = 0 , 非 齐 次 即与y相关在等号左边,与x相关在等号右边;y ′ ′ + 4 x y = 7 x y''+4xy=7x y ′ ′ + 4 x y = 7 x 7 x ≠ 0 7x\ne 0 7 x = 0 y ′ ′ + 4 x y + 7 x = 0 y''+4xy+7x=0 y ′ ′ + 4 x y + 7 x = 0
解的类型判断
C的个数与阶数相同→ \rightarrow →
不含C的解→ \rightarrow →
满足方程的解→ \rightarrow → y = C e x + 1 y=Ce^x+1 y = C e x + 1 y ′ ′ − y ′ = 0 y''-y'=0 y ′ ′ − y ′ = 0
微分方程的直接积分法 条件:遇y ( n ) = Q ( x ) y^{(n)}=Q(x) y ( n ) = Q ( x ) y ′ ′ = x + 1 y''=x+1 y ′ ′ = x + 1 y ′ ′ = x + 1 y''=x+1 y ′ ′ = x + 1 y ′ = ∫ ( x + 1 ) d x = 1 2 x 2 + x + C 1 y'=\int (x+1)dx=\frac{1}{2}x^2+x+C_1 y ′ = ∫ ( x + 1 ) d x = 2 1 x 2 + x + C 1 y = ∫ ( 1 2 x 2 + x + C 1 ) d x = 1 2 ⋅ 1 3 x 3 + 1 2 x 2 + C 1 x + C 2 y=\int (\frac{1}{2}x^2+x+C_1)dx=\frac{1}{2}\cdot \frac{1}{3}x^3+\frac{1}{2}x^2+C_1x+C_2 y = ∫ ( 2 1 x 2 + x + C 1 ) d x = 2 1 ⋅ 3 1 x 3 + 2 1 x 2 + C 1 x + C 2 y = 1 6 x 3 + 1 2 x 2 + C 1 x + C 2 y=\frac{1}{6}x^3+\frac{1}{2}x^2+C_1x+C_2 y = 6 1 x 3 + 2 1 x 2 + C 1 x + C 2
一阶微分方程求解 可分离变量微分方程的求解 当方程中x x x y y y f ( x ) d x = g ( y ) d y f(x)dx=g(y)dy f ( x ) d x = g ( y ) d y f ( x ) d x = g ( y ) d y f(x)dx=g(y)dy f ( x ) d x = g ( y ) d y ∫ f ( x ) d x = ∫ g ( y ) d y \int f(x)dx=\int g(y)dy ∫ f ( x ) d x = ∫ g ( y ) d y C 1 ± C 2 = C C_1 \pm C_2=C C 1 ± C 2 = C C 1 ⋅ C 2 C_1 \cdot C_2 C 1 ⋅ C 2 C 1 C 2 = C \frac{C_1}{C_2}=C C 2 C 1 = C C = ln C C=\ln C C = ln C ± e C = C \pm e^C=C ± e C = C d y d x = x y \frac{dy}{dx}=xy d x d y = x y d y = x y d x dy=xy dx d y = x y d x d y y = x d x \frac{dy}{y}=xdx y d y = x d x 1 y d y = x d x \frac{1}{y}dy=xdx y 1 d y = x d x ∫ 1 y d y = ∫ x d x \int \frac{1}{y}dy=\int xdx ∫ y 1 d y = ∫ x d x ln ∣ y ∣ = 1 2 x 2 + C \ln |y|=\frac{1}{2}x^2+C ln ∣ y ∣ = 2 1 x 2 + C ln ∣ y ∣ = 1 2 x 2 + C \ln |y|=\frac{1}{2}x^2+C ln ∣ y ∣ = 2 1 x 2 + C ln ∣ y ∣ = 1 2 x 2 + ln ∣ C ∣ \ln |y|=\frac{1}{2}x^2+\ln |C| ln ∣ y ∣ = 2 1 x 2 + ln ∣ C ∣ ln ∣ y ∣ − ln ∣ C ∣ = 1 2 x 2 \ln |y|-\ln |C|=\frac{1}{2}x^2 ln ∣ y ∣ − ln ∣ C ∣ = 2 1 x 2 ln ∣ y C ∣ = 1 2 x 2 \ln |\frac{y}{C}|=\frac{1}{2}x^2 ln ∣ C y ∣ = 2 1 x 2 ∣ y C ∣ = e 1 2 x 2 |\frac{y}{C}|=e^{\frac{1}{2}x^2} ∣ C y ∣ = e 2 1 x 2 y C = ± e 1 2 x 2 \frac{y}{C}=\pm e^{\frac{1}{2}x^2} C y = ± e 2 1 x 2 y = ± C e 1 2 x 2 y=\pm Ce^{\frac{1}{2}x^2} y = ± C e 2 1 x 2 y = C e x 2 2 y=Ce^{\frac{x^2}{2}} y = C e 2 x 2 d x + x y d y = y 2 d x + y d y dx+xydy=y^2dx+ydy d x + x y d y = y 2 d x + y d y ( x y − y ) d y = ( y 2 − 1 ) d x (xy-y)dy=(y^2-1)dx ( x y − y ) d y = ( y 2 − 1 ) d x y ( x − 1 ) d y = ( y 2 − 1 ) d x y(x-1)dy=(y^2-1)dx y ( x − 1 ) d y = ( y 2 − 1 ) d x y d y = ( y 2 − 1 ) x − 1 d x ydy=\frac{(y^2-1)}{x-1}dx y d y = x − 1 ( y 2 − 1 ) d x 1 y 2 − 1 , y y 2 − 1 d y = 1 x − 1 d x \frac{1}{y^2-1},\frac{y}{y^2-1}dy=\frac{1}{x-1}dx y 2 − 1 1 , y 2 − 1 y d y = x − 1 1 d x y y 2 − 1 d y = 1 x − 1 d x \frac{y}{y^2-1}dy=\frac{1}{x-1}dx y 2 − 1 y d y = x − 1 1 d x ∫ y y 2 − 1 d y = ∫ 1 x − 1 d x \int \frac{y}{y^2-1}dy=\int \frac{1}{x-1}dx ∫ y 2 − 1 y d y = ∫ x − 1 1 d x 1 2 ∫ 1 y 2 − 1 d y 2 = ∫ 1 x − 1 d x \frac{1}{2}\int \frac{1}{y^2-1}dy^2=\int \frac{1}{x-1}dx 2 1 ∫ y 2 − 1 1 d y 2 = ∫ x − 1 1 d x 1 2 ln ∣ y 2 − 1 ∣ = ln ∣ 1 x − 1 ∣ + C \frac{1}{2}\ln|y^2-1|=\ln |\frac{1}{x-1}|+C 2 1 ln ∣ y 2 − 1 ∣ = ln ∣ x − 1 1 ∣ + C 1 2 ln ∣ y 2 − 1 ∣ = ln ∣ 1 x − 1 ∣ + C \frac{1}{2}\ln|y^2-1|=\ln |\frac{1}{x-1}|+C 2 1 ln ∣ y 2 − 1 ∣ = ln ∣ x − 1 1 ∣ + C 1 2 ln ∣ y 2 − 1 ∣ = ln ∣ x − 1 ∣ + ln ∣ C ∣ \frac{1}{2}\ln |y^2-1|=\ln |x-1|+\ln |C| 2 1 ln ∣ y 2 − 1 ∣ = ln ∣ x − 1 ∣ + ln ∣ C ∣ ln ∣ y 2 − 1 ∣ 1 2 = ln ∣ C ⋅ ( x − 1 ) ∣ \ln |y^2-1|^{\frac{1}{2} }=\ln |C\cdot (x-1)| ln ∣ y 2 − 1 ∣ 2 1 = ln ∣ C ⋅ ( x − 1 ) ∣ ( y 2 − 1 ) 1 2 = C ⋅ ( x − 1 ) (y^2-1)^{\frac{1}{2} }=C\cdot (x-1) ( y 2 − 1 ) 2 1 = C ⋅ ( x − 1 ) y 2 − 1 = C ⋅ ( x − 1 ) \sqrt{y^2-1}=C\cdot (x-1) y 2 − 1 = C ⋅ ( x − 1 ) y 2 − 1 = C 2 ⋅ ( x − 1 ) 2 y^2-1=C^2\cdot (x-1)^2 y 2 − 1 = C 2 ⋅ ( x − 1 ) 2 y 2 = C 2 ⋅ ( x − 1 ) 2 + 1 y^2=C^2\cdot (x-1)^2+1 y 2 = C 2 ⋅ ( x − 1 ) 2 + 1 y 2 = C ⋅ ( x − 1 ) 2 + 1 y^2=C\cdot (x-1)^2+1 y 2 = C ⋅ ( x − 1 ) 2 + 1
一阶齐次微分方程 解法:d y d x = φ ( y x ) \frac{dy}{dx}=\varphi (\frac{y}{x}) d x d y = φ ( x y ) y x = u \frac{y}{x}=u x y = u y = u ⋅ x ⟹ y ′ = u ′ x + u y=u \cdot x \Longrightarrow y'=u'x+u y = u ⋅ x ⟹ y ′ = u ′ x + u d y d x = d y d x ⋅ x + u \frac{dy}{dx}=\frac{dy}{dx}\cdot x+u d x d y = d x d y ⋅ x + u y x = φ ( y x ) \frac{y}{x}=\varphi (\frac{y}{x}) x y = φ ( x y ) u = y x u=\frac{y}{x} u = x y y 2 + x 2 d y d x = x y d y d x y^2+x^2\frac{dy}{dx}=xy\frac{dy}{dx} y 2 + x 2 d x d y = x y d x d y y 2 = ( x y − x 2 ) d y d x ⟹ 同除 x 2 , ( y x ) 2 = ( y x − 1 ) d y d x y^2=(xy-x^2)\frac{dy}{dx}\Longrightarrow 同除x^2 ,(\frac{y}{x})^2=(\frac{y}{x}-1)\frac{dy }{dx} y 2 = ( x y − x 2 ) d x d y ⟹ 同 除 x 2 , ( x y ) 2 = ( x y − 1 ) d x d y ( y x ) 2 = ( y x − 1 ) d y d x (\frac{y}{x})^2=(\frac{y}{x}-1)\frac{dy}{dx} ( x y ) 2 = ( x y − 1 ) d x d y y x = u , y = u ⋅ x , d y d x = d u d x ⋅ x + u \frac{y}{x}=u,y=u\cdot x,\frac{dy}{dx}=\frac{du}{dx}\cdot x+u x y = u , y = u ⋅ x , d x d y = d x d u ⋅ x + u u 2 = ( u − 1 ) ( x d u d x + u ) u^2=(u-1)(x\frac{du}{dx}+u) u 2 = ( u − 1 ) ( x d x d u + u ) u 2 = ( u − 1 ) x d u d x + u 2 − u u^2=(u-1)x\frac{du}{dx}+u^2-u u 2 = ( u − 1 ) x d x d u + u 2 − u u = ( u − 1 ) x d u d x u=(u-1)x\frac{du}{dx} u = ( u − 1 ) x d x d u u d x = ( u − 1 ) x d u udx=(u-1)xdu u d x = ( u − 1 ) x d u u x , 1 x d x = ( u − 1 ) u d u ux,\frac{1}{x}dx=\frac{(u-1)}{u}du u x , x 1 d x = u ( u − 1 ) d u 1 x d x = ( 1 − ( 1 ) u ) d u \frac{1}{x}dx=(1-\frac{(1)}{u})du x 1 d x = ( 1 − u ( 1 ) ) d u ∫ 1 x d x = ∫ ( 1 − ( 1 ) u ) d u \int \frac{1}{x}dx=\int (1-\frac{(1)}{u})du ∫ x 1 d x = ∫ ( 1 − u ( 1 ) ) d u ln ∣ x ∣ = u − ln ∣ u ∣ + C \ln |x|=u-\ln |u|+C ln ∣ x ∣ = u − ln ∣ u ∣ + C ln ∣ x ∣ = y x − ln ∣ y x ∣ + C \ln |x|=\frac{y}{x}-\ln |\frac{y}{x}|+C ln ∣ x ∣ = x y − ln ∣ x y ∣ + C ln ∣ x ∣ + ln ∣ y x ∣ − C = y x \ln |x|+\ln |\frac{y}{x}|-C=\frac{y}{x} ln ∣ x ∣ + ln ∣ x y ∣ − C = x y ln ∣ y ∣ − ln ∣ C ∣ = y x \ln |y|-\ln |C|=\frac{y}{x} ln ∣ y ∣ − ln ∣ C ∣ = x y ln ∣ y C ∣ = y x \ln |\frac{y}{C}|=\frac{y}{x} ln ∣ C y ∣ = x y ∣ y C ∣ = e y x |\frac{y}{C}|=e^{\frac{y}{x} } ∣ C y ∣ = e x y y C = ± e y x \frac{y}{C}=\pm e^{\frac{y}{x} } C y = ± e x y y = ± C e y x y=\pm Ce^{\frac{y}{x} } y = ± C e x y y = C e y x y=Ce^{\frac{y}{x} } y = C e x y
一阶线性微分方程
形式:y ′ + P ( x ) ⋅ y = Q ( x ) y'+P(x)\cdot y=Q(x) y ′ + P ( x ) ⋅ y = Q ( x ) y = e − ∫ P ( x ) d x ⋅ [ ∫ Q ( x ) e ∫ P ( x ) d x d x + C ] y=e^{-\int P(x)dx}\cdot [\int Q(x)e^{\int P(x)dx}dx+C] y = e − ∫ P ( x ) d x ⋅ [ ∫ Q ( x ) e ∫ P ( x ) d x d x + C ]
形式:x ′ + P ( y ) ⋅ x = Q ( y ) x'+P(y)\cdot x=Q(y) x ′ + P ( y ) ⋅ x = Q ( y ) x = e − ∫ P ( y ) d y ⋅ [ ∫ Q ( y ) e ∫ P ( y ) d y d y + C ] x=e^{-\int P(y)dy}\cdot [\int Q(y)e^{\int P(y)dy}dy+C] x = e − ∫ P ( y ) d y ⋅ [ ∫ Q ( y ) e ∫ P ( y ) d y d y + C ] y ′ + y = e − x y'+y=e^{-x} y ′ + y = e − x P ( x ) = 1 , Q ( x ) = e − x P(x)=1,Q(x)=e^{-x} P ( x ) = 1 , Q ( x ) = e − x y = e − ∫ P ( x ) d x [ ∫ Q ( x ) e ∫ P ( x ) d x d x + C ] y=e^{-\int P(x)dx}[\int Q(x)e^{\int P(x)dx}dx+C] y = e − ∫ P ( x ) d x [ ∫ Q ( x ) e ∫ P ( x ) d x d x + C ] e − ∫ 1 d x [ ∫ e − x ⋅ e ∫ 1 d x d x + C ] e^{-\int 1dx}[\int e^{-x}\cdot e^{\int 1dx}dx+C] e − ∫ 1 d x [ ∫ e − x ⋅ e ∫ 1 d x d x + C ] e − x [ ∫ e − x ⋅ e x d x + C ] e^{-x}[\int e^{-x}\cdot e^xdx+C] e − x [ ∫ e − x ⋅ e x d x + C ] e − x ( x + C ) ] e^{-x}(x+C)] e − x ( x + C ) ] y y y y ′ y' y ′ y ′ + P y = Q y'+Py=Q y ′ + P y = Q ( x 2 − 1 ) ⋅ y ′ + 2 x y − cos x = 0 (x^2-1)\cdot y'+2xy-\cos x=0 ( x 2 − 1 ) ⋅ y ′ + 2 x y − cos x = 0 y ′ + 2 x x 2 − 1 ⋅ y − cos x x 2 − 1 = 0 ⟹ y ′ + 2 x x 2 + 1 ⋅ y = cos x x 2 − 1 x 2 − 1 y'+\frac{2x}{x^2-1}\cdot y-\frac{\cos x}{x^2-1}=0 \Longrightarrow y'+\frac{2x}{x^2+1}\cdot y=\frac{\cos x}{x^2-1}{x^2-1} y ′ + x 2 − 1 2 x ⋅ y − x 2 − 1 c o s x = 0 ⟹ y ′ + x 2 + 1 2 x ⋅ y = x 2 − 1 c o s x x 2 − 1 y ′ + 2 x x 2 − 1 ⋅ y = cos x x 2 − 1 y'+\frac{2x}{x^2-1}\cdot y = \frac{\cos x}{x^2-1} y ′ + x 2 − 1 2 x ⋅ y = x 2 − 1 c o s x P ( x ) = 2 x x 2 − 1 , Q ( x ) = cos x x 2 − 1 P(x)=\frac{2x}{x^2-1},Q(x)=\frac{\cos x}{x^2-1} P ( x ) = x 2 − 1 2 x , Q ( x ) = x 2 − 1 c o s x y = e − ∫ P ( x ) d x [ ∫ Q ( x ) ⋅ e ∫ P ( x ) d x d x + C ] y=e^{-\int P(x)dx}[\int Q(x)\cdot e^{\int P(x)dx}dx+C] y = e − ∫ P ( x ) d x [ ∫ Q ( x ) ⋅ e ∫ P ( x ) d x d x + C ] = e − ∫ 2 x x 2 − 1 d x [ ∫ cos x x 2 − 1 ⋅ e ∫ 2 x x 2 − 1 d x d x + C ] =e^{-\int \frac{2x}{x^2-1}dx}[\int \frac{\cos x}{x^2-1}\cdot e^{\int \frac{2x}{x^2-1}dx}dx+C] = e − ∫ x 2 − 1 2 x d x [ ∫ x 2 − 1 c o s x ⋅ e ∫ x 2 − 1 2 x d x d x + C ] = e − ln ( x 2 − 1 ) [ ∫ cos x x 2 − 1 ⋅ e ln ( x 2 − 1 ) d x + C ] =e^{-\ln (x^2-1)}[\int \frac{\cos x}{x^2-1}\cdot e^{\ln (x^2-1)}dx+C] = e − l n ( x 2 − 1 ) [ ∫ x 2 − 1 c o s x ⋅ e l n ( x 2 − 1 ) d x + C ] = e ln ( x 2 − 1 ) − 1 [ ∫ cos x x 2 − 1 ⋅ e ln ( x 2 − 1 ) d x + C ] =e^{\ln (x^2-1)^{-1} }[\int \frac{\cos x}{x^2-1}\cdot e^{\ln (x^2-1)}dx+C] = e l n ( x 2 − 1 ) − 1 [ ∫ x 2 − 1 c o s x ⋅ e l n ( x 2 − 1 ) d x + C ] = ( x 2 − 1 ) − 1 [ ∫ cos x x 2 − 1 ⋅ ln ( x 2 − 1 ) d x + C ] =(x^2-1)^{-1} [\int \frac{\cos x}{x^2-1}\cdot \ln (x^2-1)dx+C] = ( x 2 − 1 ) − 1 [ ∫ x 2 − 1 c o s x ⋅ ln ( x 2 − 1 ) d x + C ] = 1 x 2 − 1 ( ∫ cos x d x + C ) =\frac{1}{x^2-1} (\int \cos xdx+C) = x 2 − 1 1 ( ∫ cos x d x + C ) = 1 x 2 − 1 ( sin x + C ) =\frac{1}{x^2-1} (\sin x+C) = x 2 − 1 1 ( sin x + C ) e ln □ = □ {\color{Red} e^{\ln \Box }=\Box } e l n □ = □
变限积分中的微分方程 遇变限积分:(1). 求导; (2). 用∫ a b f ( t ) d t = 0 ⟹ \int_{a}^{b} f(t)dt=0\Longrightarrow ∫ a b f ( t ) d t = 0 ⟹ f ( x ) f(x) f ( x ) f ( x ) = ∫ 0 x f ( t ) d t + e x f(x)=\int_{0}^{x}f(t)dt+e^x f ( x ) = ∫ 0 x f ( t ) d t + e x f ( x ) f(x) f ( x ) f ′ ( x ) = f ( x ) + e x f'(x)=f(x)+e^x f ′ ( x ) = f ( x ) + e x x = 0 x=0 x = 0 f ( 0 ) = 1 f(0)=1 f ( 0 ) = 1 f ( x ) = y f(x)=y f ( x ) = y y ′ − y = e x y'-y=e^x y ′ − y = e x P ( x ) = − 1 , Q ( x ) = e x P(x)=-1,Q(x)=e^x P ( x ) = − 1 , Q ( x ) = e x e − x f ( x ) = ∫ 1 d x + C e^{-x}f(x)=\int 1dx+C e − x f ( x ) = ∫ 1 d x + C e − x f ( x ) = x + C e^{-x}f(x)=x+C e − x f ( x ) = x + C f ( x ) = e x ( x + C ) f(x)=e^x(x+C) f ( x ) = e x ( x + C ) y = e − ∫ P ( x ) d x [ ∫ Q ( x ) ⋅ e ∫ P ( x ) d x d x + C ] y=e^{-\int P(x)dx}[\int Q(x)\cdot e^{\int P(x)dx}dx+C] y = e − ∫ P ( x ) d x [ ∫ Q ( x ) ⋅ e ∫ P ( x ) d x d x + C ] = e − ∫ − 1 d x [ ∫ e x ⋅ e ∫ − 1 d x d x + C ] =e^{-\int -1dx}[\int e^x\cdot e^{\int -1dx}dx+C] = e − ∫ − 1 d x [ ∫ e x ⋅ e ∫ − 1 d x d x + C ] = e x [ ∫ e x ⋅ e − x d x + C ] =e^x[\int e^x\cdot e^{-x}dx+C] = e x [ ∫ e x ⋅ e − x d x + C ] = e x ( x + C ) =e^x(x+C) = e x ( x + C ) x = 0 , y = 1 x=0,y=1 x = 0 , y = 1 1 = e 0 ( 0 + C ) 1=e^0(0+C) 1 = e 0 ( 0 + C ) C = 1 C=1 C = 1 y = e x ( x + 1 ) y=e^x(x+1) y = e x ( x + 1 ) f ( x ) f(x) f ( x ) f ( 0 ) = 0 f(0)=0 f ( 0 ) = 0 ∫ 2 [ f ( x ) − e x ] y d x − f ( x ) d y \int_{2}[f(x)-e^x]ydx-f(x)dy ∫ 2 [ f ( x ) − e x ] y d x − f ( x ) d y f ( x ) f(x) f ( x ) P ( x , y ) = [ f ( x ) − e x ] ⋅ y , Q ( x , y ) = − f ( x ) P(x,y)=[f(x)-e^x]\cdot y,Q(x,y)=-f(x) P ( x , y ) = [ f ( x ) − e x ] ⋅ y , Q ( x , y ) = − f ( x ) P y = Q x \frac{P}{y}=\frac{Q}{x} y P = x Q f ( x ) − e x = − f ′ ( x ) f(x)-e^x=-f'(x) f ( x ) − e x = − f ′ ( x ) y − e x = − y ′ y-e^x=-y' y − e x = − y ′ y ′ + y = e x y'+y=e^x y ′ + y = e x P ( x ) = 1 , Q ( x ) = e x P(x)=1,Q(x)=e^x P ( x ) = 1 , Q ( x ) = e x y = e − ∫ P ( x ) d x [ ∫ Q ( x ) ⋅ e ∫ P ( x ) d x d x + C ] y=e^{-\int P(x)dx}[\int Q(x)\cdot e^{\int P(x)dx}dx+C] y = e − ∫ P ( x ) d x [ ∫ Q ( x ) ⋅ e ∫ P ( x ) d x d x + C ] y = e − ∫ 1 d x [ ∫ e x ⋅ e ∫ 1 d x d x + C ] y=e^{-\int 1dx}[\int e^x\cdot e^{\int 1dx}dx+C] y = e − ∫ 1 d x [ ∫ e x ⋅ e ∫ 1 d x d x + C ] y = e − x [ ∫ e x ⋅ e x d x + C ] y=e^{-x}[\int e^x\cdot e^x dx+C] y = e − x [ ∫ e x ⋅ e x d x + C ] y = e − x [ 1 2 ∫ e 2 x d 2 x + C ] y=e^{-x}[\frac{1}{2}\int e^{2x}d2x+C] y = e − x [ 2 1 ∫ e 2 x d 2 x + C ] y = e − x ( 1 2 e 2 x + C ) y=e^{-x}(\frac{1}{2}e^{2x}+C) y = e − x ( 2 1 e 2 x + C ) f ( x ) = y = e − x ( 1 2 e 2 x + C ) f(x)=y=e^{-x}(\frac{1}{2}e^{2x}+C) f ( x ) = y = e − x ( 2 1 e 2 x + C ) f ( 0 ) = 0 f(0)=0 f ( 0 ) = 0 0 = e − 0 ( 1 2 e 2 ⋅ 0 + C ) 0=e^{-0}(\frac{1}{2}e^{2\cdot 0}+C) 0 = e − 0 ( 2 1 e 2 ⋅ 0 + C ) C = − 1 2 C=-\frac{1}{2} C = − 2 1 f ( x ) = y = e − x ( 1 2 e 2 x − 1 2 ) f(x)=y=e^{-x}(\frac{1}{2}e^{2x}-\frac{1}{2}) f ( x ) = y = e − x ( 2 1 e 2 x − 2 1 )
二阶微分方程 二阶线性微分方程
定义:称a y ′ ′ + b y ′ + c y = f ( x ) ay''+by'+cy=f(x) a y ′ ′ + b y ′ + c y = f ( x ) f ( x ) = 0 f(x)=0 f ( x ) = 0 f ( x ) = P ( x ) ⋅ e λ x f(x)=P(x)\cdot e^{\lambda x} f ( x ) = P ( x ) ⋅ e λ x
二阶齐次微分方程的解法a y ′ ′ + b y ′ + c y = 0 ay''+by'+cy=0 a y ′ ′ + b y ′ + c y = 0 a r 2 + b r + c = 0 ar^2+br+c=0 a r 2 + b r + c = 0 r 1 , 2 = − b ± b 2 − 4 a c 2 a r_{1,2}=\frac{-b \pm \sqrt{b^2-4ac} }{2a} r 1 , 2 = 2 a − b ± b 2 − 4 a c { 1. r 1 ≠ r 2 , y = c 1 e r 1 x + c 2 e r 2 x 2. r 1 = r 2 , y = ( c 1 + c 2 x ) e r 1 x 3. r 1 , 2 = a ± b i , y = e a x ⋅ ( c 1 cos b x + c 2 sin b x ) \left\{\begin{matrix}1. r_1 \ne r_2,y=c_1e^{r_1x}+c_2e^{r_2x}\\2. r_1=r_2,y=(c_1+c_2x)e^{r_1x}\\3.r_{1,2}=a \pm bi,y=e^{ax}\cdot (c_1\cos bx+c_2\sin bx) \end{matrix}\right. ⎩ ⎪ ⎨ ⎪ ⎧ 1 . r 1 = r 2 , y = c 1 e r 1 x + c 2 e r 2 x 2 . r 1 = r 2 , y = ( c 1 + c 2 x ) e r 1 x 3 . r 1 , 2 = a ± b i , y = e a x ⋅ ( c 1 cos b x + c 2 sin b x ) i 2 = − 1 i^2=-1 i 2 = − 1 − 4 = 4 i = 2 i \sqrt{-4}=\sqrt{4i}=2i − 4 = 4 i = 2 i y ′ ′ + 5 y ′ + 6 y = 0 y''+5y'+6y=0 y ′ ′ + 5 y ′ + 6 y = 0 r 2 + 5 r + 6 = 0 r^2+5r+6=0 r 2 + 5 r + 6 = 0 r 1 = − 2 , r 2 = − 3 r_1=-2,r_2=-3 r 1 = − 2 , r 2 = − 3 y = c 1 e − 2 x + c 2 e − 3 x y=c_1e^{-2x}+c_2e^{-3x} y = c 1 e − 2 x + c 2 e − 3 x y = c 1 e − 3 x + c 2 x e − 2 x y=c_1e^{-3x}+c_2xe^{-2x} y = c 1 e − 3 x + c 2 x e − 2 x y ′ ′ + 6 y ′ + 9 y = 0 y''+6y'+9y=0 y ′ ′ + 6 y ′ + 9 y = 0 r 2 + 6 r + 9 = 0 r^2+6r+9=0 r 2 + 6 r + 9 = 0 r 1 = r 2 = − 3 r_1=r_2=-3 r 1 = r 2 = − 3 y = ( c 1 + c 2 x ) e − 3 x y=(c_1+c_2x)e^{-3x} y = ( c 1 + c 2 x ) e − 3 x y ′ ′ − 4 y ′ + 5 y = 0 y''-4y'+5y=0 y ′ ′ − 4 y ′ + 5 y = 0 r 2 − 4 r + 5 = 0 r^2-4r+5=0 r 2 − 4 r + 5 = 0 r 1 , 2 = 2 ± 1 i r_{1,2}=2\pm 1i r 1 , 2 = 2 ± 1 i y = e 2 x ( c 1 cos x + c 2 sin x ) y=e^{2x}(c_1\cos x+c_2\sin x) y = e 2 x ( c 1 cos x + c 2 sin x ) y ′ ′ + 6 y ′ + 9 y = 0 y''+6y'+9y=0 y ′ ′ + 6 y ′ + 9 y = 0 y ∣ x = 0 = 1 , y ′ ∣ x = 0 = 2 y|_{x=0}=1,y'|_{x=0}=2 y ∣ x = 0 = 1 , y ′ ∣ x = 0 = 2 r 2 + 6 r + 9 = 0 r^2+6r+9=0 r 2 + 6 r + 9 = 0 r 1 = r 2 = 3 r_1=r_2=3 r 1 = r 2 = 3 y = ( c 1 + c 2 x ) e 3 x y=(c_1+c_2x)e^{3x} y = ( c 1 + c 2 x ) e 3 x y ′ = c 2 e 3 x + ( c 1 + c 2 x ) e 3 x ⋅ 3 y'=c_2e^{3x}+(c_1+c_2x)e^{3x}\cdot 3 y ′ = c 2 e 3 x + ( c 1 + c 2 x ) e 3 x ⋅ 3 y ∣ x = 0 = 1 , y ′ ∣ x = 0 = 2 y|_{x=0}=1,y'|_{x=0}=2 y ∣ x = 0 = 1 , y ′ ∣ x = 0 = 2 c 1 = 1 , c 2 = − 1 c_1=1,c_2=-1 c 1 = 1 , c 2 = − 1 c 1 c_1 c 1 c 2 c_2 c 2 y = c 1 e − x + c 2 e 5 x y=c_1e^{-x}+c_2e^{5x} y = c 1 e − x + c 2 e 5 x r 1 = − 1 , r 2 = 5 r_1=-1,r_2=5 r 1 = − 1 , r 2 = 5 ( r + 1 ) ( r − 5 ) = 0 (r+1)(r-5)=0 ( r + 1 ) ( r − 5 ) = 0 r 2 − 4 r − 5 = 0 r^2-4r-5=0 r 2 − 4 r − 5 = 0 y ′ ′ − 4 y ′ − 5 y = 0 y''-4y'-5y=0 y ′ ′ − 4 y ′ − 5 y = 0
二阶常系数非齐次线性微分方程 特解的一般形式
定义:a y ′ ′ + b y ′ + c y = f ( x ) ay''+by'+cy=f(x) a y ′ ′ + b y ′ + c y = f ( x )
类型:a y ′ ′ + b y ′ + c y = P ( x ) ⋅ e λ x ay''+by'+cy=P(x)\cdot e^{\lambda x} a y ′ ′ + b y ′ + c y = P ( x ) ⋅ e λ x y = y ˉ + y ∗ y=\bar{y}+y^* y = y ˉ + y ∗ y ˉ \bar{y} y ˉ y ∗ y^* y ∗ y ˉ : a y ′ ′ + b y ′ + c y = 0 \bar{y}:ay''+by'+cy=0 y ˉ : a y ′ ′ + b y ′ + c y = 0 − > a y ˉ ′ ′ + b y ˉ ′ + c y ˉ = 0 ->a\bar{y}''+b\bar{y}'+c\bar{y}=0 − > a y ˉ ′ ′ + b y ˉ ′ + c y ˉ = 0 y ∗ : a y ′ ′ + b y ′ + c y = P ( x ) ⋅ e λ x y^*:ay''+by'+cy=P(x)\cdot e^{\lambda x} y ∗ : a y ′ ′ + b y ′ + c y = P ( x ) ⋅ e λ x a y ∗ ′ ′ + b y ∗ ′ + c y ∗ = P ( x ) ⋅ e λ x a{y^*}''+b{y^*}'+cy^*=P(x)\cdot e^{\lambda x} a y ∗ ′ ′ + b y ∗ ′ + c y ∗ = P ( x ) ⋅ e λ x a ( y ˉ ′ ′ + y ∗ ′ ′ ) + b ( y ˉ ′ + y ∗ ′ ) + c ( y ˉ + y ∗ ) = P ( x ) ⋅ e λ x a({\bar{y} }''+{y^*}'')+b({\bar{y} }'+{y^*}')+c(\bar{y}+y^*)=P(x)\cdot e^{\lambda x} a ( y ˉ ′ ′ + y ∗ ′ ′ ) + b ( y ˉ ′ + y ∗ ′ ) + c ( y ˉ + y ∗ ) = P ( x ) ⋅ e λ x a y ′ ′ + b y ′ + c y = P ( x ) ⋅ e λ x ay''+by'+cy=P(x)\cdot e^{\lambda x} a y ′ ′ + b y ′ + c y = P ( x ) ⋅ e λ x
求二阶非齐次通解:a y ′ ′ + b y ′ + c y = 0 ay''+by'+cy=0 a y ′ ′ + b y ′ + c y = 0 y ˉ \bar{y} y ˉ y ∗ y^* y ∗ y ∗ ′ , y ∗ ′ ′ {y^*}',{y^*}'' y ∗ ′ , y ∗ ′ ′ y ∗ , y ∗ ′ , y ∗ ′ ′ y^*,{y^*}',{y^*}'' y ∗ , y ∗ ′ , y ∗ ′ ′ a y ′ ′ + b y ′ + c y = P ( x ) ⋅ e λ x ay''+by'+cy=P(x)\cdot e^{\lambda x} a y ′ ′ + b y ′ + c y = P ( x ) ⋅ e λ x a y ∗ ′ ′ + b y ∗ ′ + c y ∗ = P ( x ) ⋅ e λ x a{y^*}''+b{y^*}'+cy^*=P(x)\cdot e^{\lambda x} a y ∗ ′ ′ + b y ∗ ′ + c y ∗ = P ( x ) ⋅ e λ x y ∗ y^* y ∗ y = y ˉ + y ∗ y=\bar{y}+y^* y = y ˉ + y ∗ y ∗ y^* y ∗ P ( x ) ⋅ e λ x P(x)\cdot e^{\lambda x} P ( x ) ⋅ e λ x y ∗ = Q ( x ) ⋅ e λ x ⋅ x k y^*=Q(x)\cdot e^{\lambda x}\cdot x^k y ∗ = Q ( x ) ⋅ e λ x ⋅ x k Q ( x ) Q(x) Q ( x ) P ( x ) P(x) P ( x ) P ( x ) P(x) P ( x ) A , B A,B A , B = Q ( x ) =Q(x) = Q ( x ) a x + b = Q ( x ) ax+b=Q(x) a x + b = Q ( x ) a x 2 + b x + c = Q ( x ) ax^2+bx+c=Q(x) a x 2 + b x + c = Q ( x ) x k x^k x k k k k λ \lambda λ r 1 , r 2 r_1,r_2 r 1 , r 2 k = 0 , λ ≠ r 1 , λ ≠ r 2 k=0,\lambda \ne r_1,\lambda \ne r_2 k = 0 , λ = r 1 , λ = r 2 k = 1 , λ k=1,\lambda k = 1 , λ r 1 r 2 r_1 r_2 r 1 r 2 k = 2 , λ = r 1 , λ = r 2 k=2,\lambda = r_1,\lambda = r_2 k = 2 , λ = r 1 , λ = r 2 y ′ ′ − 5 y ′ + 6 y = 3 x e 2 x y''-5y'+6y=3xe^{2x} y ′ ′ − 5 y ′ + 6 y = 3 x e 2 x P ( x ) = 3 x , Q ( x ) = e 2 x P(x)=3x,Q(x)=e^{2x} P ( x ) = 3 x , Q ( x ) = e 2 x λ = 2 , 3 x \lambda =2,3x λ = 2 , 3 x ( a x + b ) (ax+b) ( a x + b ) y ∗ = ( a x + b ) e 2 x ⋅ x k y^*=(ax+b)e^{2x}\cdot x^k y ∗ = ( a x + b ) e 2 x ⋅ x k y ′ ′ − 5 y ′ + 6 y = r 2 − 5 r + 6 = ( r − 2 ) ( r − 3 ) = 0 y''-5y'+6y=r^2-5r+6=(r-2)(r-3)=0 y ′ ′ − 5 y ′ + 6 y = r 2 − 5 r + 6 = ( r − 2 ) ( r − 3 ) = 0 r 1 = 2 , r 2 = 3 r_1=2,r_2=3 r 1 = 2 , r 2 = 3 λ = r 1 = 2 ≠ r 2 = 3 \lambda =r_1=2 \ne r_2=3 λ = r 1 = 2 = r 2 = 3 k = 1 k=1 k = 1 y ∗ = ( a x + b ) e 2 x ⋅ x y^*=(ax+b)e^{2x}\cdot x y ∗ = ( a x + b ) e 2 x ⋅ x y ∗ = ( a x 2 + b x ) e 2 x y^*=(ax^2+bx)e^{2x} y ∗ = ( a x 2 + b x ) e 2 x y ′ ′ − 5 y ′ + 6 y = 3 x e 2 x y''-5y'+6y=3xe^{2x} y ′ ′ − 5 y ′ + 6 y = 3 x e 2 x ( a x + b ) e − x (ax+b)e^{-x} ( a x + b ) e − x x 2 ( a x + b ) e − x x^2(ax+b)e^{-x} x 2 ( a x + b ) e − x x ( a x + b ) e − x x(ax+b)e^{-x} x ( a x + b ) e − x a ( x + 1 ) e − x a(x+1)e^{-x} a ( x + 1 ) e − x P ( x ) = ( x − 1 ) , Q ( x ) = e − x P(x)=(x-1),Q(x)=e^{-x} P ( x ) = ( x − 1 ) , Q ( x ) = e − x λ = − 1 , ( x − 1 ) \lambda =-1,(x-1) λ = − 1 , ( x − 1 ) ( a x + b ) (ax+b) ( a x + b ) y ∗ = ( a x + b ) e − x ⋅ x k y^*=(ax+b)e^{-x}\cdot x^k y ∗ = ( a x + b ) e − x ⋅ x k y ′ ′ + 2 y ′ + y = r 2 + 2 r + 1 = ( r + 1 ) 2 = 0 y''+2y'+y=r^2+2r+1=(r+1)^2=0 y ′ ′ + 2 y ′ + y = r 2 + 2 r + 1 = ( r + 1 ) 2 = 0 r 1 = r 2 = − 1 r_1=r_2=-1 r 1 = r 2 = − 1 λ = r 1 = − 1 = r 2 = − 1 \lambda =r_1=-1 = r_2=-1 λ = r 1 = − 1 = r 2 = − 1 k = 2 k=2 k = 2 y ∗ = x 2 ( a x + b ) e − x y^*=x^2(ax+b)e^{-x} y ∗ = x 2 ( a x + b ) e − x
题型二:非齐次通解的解及其结构 例题1:设y 1 , y 2 , y 3 y_1,y_2,y_3 y 1 , y 2 , y 3 A x = b Ax=b A x = b y 1 + y 2 + y 3 y_1+y_2+y_3 y 1 + y 2 + y 3 A x = b Ax=b A x = b y 1 − y 2 y_1-y_2 y 1 − y 2 A x = b Ax=b A x = b 2 y 1 − y 2 2y_1-y_2 2 y 1 − y 2 A x = 0 Ax=0 A x = 0 y 1 + y 2 − y 3 y_1+y_2-y_3 y 1 + y 2 − y 3 A x = b Ax=b A x = b 结构 :y ˉ + y ∗ \bar{y}+y^* y ˉ + y ∗ A y 1 = b , A y 2 = b , A y 3 = b Ay_1=b,Ay_2=b,Ay_3=b A y 1 = b , A y 2 = b , A y 3 = b A ( y 1 + y 2 + y 3 ) = 3 b A(y_1+y_2+y_3)=3b A ( y 1 + y 2 + y 3 ) = 3 b A ( y 1 − y 2 ) = 0 A(y_1-y_2)=0 A ( y 1 − y 2 ) = 0 A ( 2 y 1 − y 2 ) = b A(2y_1-y_2)=b A ( 2 y 1 − y 2 ) = b A ( y 1 + y 2 − y 3 ) = b A(y_1+y_2-y_3)=b A ( y 1 + y 2 − y 3 ) = b α 1 , α 2 \alpha _1,\alpha _2 α 1 , α 2 A x = B Ax=B A x = B β \beta β A x = 0 Ax=0 A x = 0 2 β + α 1 2\beta +\alpha _1 2 β + α 1 A x = 0 Ax=0 A x = 0 β + α 1 + α 2 \beta +\alpha _1+\alpha _2 β + α 1 + α 2 A x = 0 Ax=0 A x = 0 2 α 1 + α 2 2\alpha _1+\alpha _2 2 α 1 + α 2 A x = B Ax=B A x = B 2 α 1 − α 2 2\alpha _1-\alpha _2 2 α 1 − α 2 A x = B Ax=B A x = B A α 1 = B , A α 2 = B , A β = 0 A\alpha _1=B,A\alpha _2=B,A\beta =0 A α 1 = B , A α 2 = B , A β = 0 A ( 2 β + α 1 ) = B A(2\beta +\alpha _1)=B A ( 2 β + α 1 ) = B A ( β + α 1 + α 2 ) = 2 B A(\beta +\alpha _1+\alpha _2)=2B A ( β + α 1 + α 2 ) = 2 B A ( 2 α 1 + α 2 ) = 3 B A(2\alpha _1+\alpha _2)=3B A ( 2 α 1 + α 2 ) = 3 B A ( 2 α 1 − α 2 ) = B A(2\alpha _1-\alpha _2)=B A ( 2 α 1 − α 2 ) = B 结构定理:a y ′ ′ + b y ′ + c y = f ( x ) ay''+by'+cy=f(x) a y ′ ′ + b y ′ + c y = f ( x ) y = y ˉ + y ∗ y=\bar{y}+y^* y = y ˉ + y ∗ y 1 , y 2 y_1,y_2 y 1 , y 2 a y ′ ′ + b y ′ + c y = f ( x ) ay''+by'+cy=f(x) a y ′ ′ + b y ′ + c y = f ( x ) y 1 − y 2 y_1-y_2 y 1 − y 2 a y ′ ′ + b y ′ + c y = 0 ay''+by'+cy=0 a y ′ ′ + b y ′ + c y = 0 y 1 ∗ , y 2 ∗ y_1^*,y_2^* y 1 ∗ , y 2 ∗ a y ′ ′ + b y ′ + c y = f 1 ( x ) ay''+by'+cy=f_1(x) a y ′ ′ + b y ′ + c y = f 1 ( x ) a y ′ ′ + b y ′ + c y = f 2 ( x ) ay''+by'+cy=f_2(x) a y ′ ′ + b y ′ + c y = f 2 ( x ) y 1 ∗ + y 2 ∗ y_1^*+y_2^* y 1 ∗ + y 2 ∗ a y ′ ′ + b y ′ + c y = f 1 ( x ) + f 2 ( x ) ay''+by'+cy=f_1(x)+f_2(x) a y ′ ′ + b y ′ + c y = f 1 ( x ) + f 2 ( x ) y 1 , y 2 y_1,y_2 y 1 , y 2 a y ′ ′ + b y ′ + c y = f ( x ) ay''+by'+cy=f(x) a y ′ ′ + b y ′ + c y = f ( x ) y 1 − y 2 y_1-y_2 y 1 − y 2 a y ′ ′ + b y ′ + c y = 0 ay''+by'+cy=0 a y ′ ′ + b y ′ + c y = 0 c 1 y 1 + c 2 y 2 + y 1 ( y 2 ) = > a y ′ ′ + b y ′ + c y = f ( x ) c_1y_1+c_2y_2+y_1(y_2)=>ay''+by'+cy=f(x) c 1 y 1 + c 2 y 2 + y 1 ( y 2 ) = > a y ′ ′ + b y ′ + c y = f ( x )
非齐次微分方程求通解 例题1:求微分方程y ′ ′ − 5 y ′ + 6 y = x e 2 x y''-5y'+6y=xe^{2x} y ′ ′ − 5 y ′ + 6 y = x e 2 x r 2 − 5 r + 6 = ( r − 2 ) ( r − 3 ) = 0 r^2-5r+6=(r-2)(r-3)=0 r 2 − 5 r + 6 = ( r − 2 ) ( r − 3 ) = 0 r 1 = 2 , r 2 = 3 r_1=2,r_2=3 r 1 = 2 , r 2 = 3 y = c 1 e 2 x + c 2 e 3 x y=c_1e^{2x}+c_2e^{3x} y = c 1 e 2 x + c 2 e 3 x λ = 2 = r 1 ≠ r 1 \lambda =2=r_1 \ne r_1 λ = 2 = r 1 = r 1 k = 1 k=1 k = 1 y ∗ = ( a x + b ) e 2 x ⋅ x y^*=(ax+b)e^{2x}\cdot x y ∗ = ( a x + b ) e 2 x ⋅ x y ∗ = ( a x 2 + b x ) e 2 x y^*=(ax^2+bx)e^{2x} y ∗ = ( a x 2 + b x ) e 2 x y ∗ ′ ′ − 5 y ∗ ′ + 6 y ∗ = ( − 2 a x + 2 a − b ) e 2 x = x e 2 x {y^*}''-5{y^*}'+6y^*=(-2ax+2a-b)e^{2x}=xe^{2x} y ∗ ′ ′ − 5 y ∗ ′ + 6 y ∗ = ( − 2 a x + 2 a − b ) e 2 x = x e 2 x a = − 1 2 , b = − 1 a=-\frac{1}{2},b=-1 a = − 2 1 , b = − 1 y ∗ = − 1 2 x 2 e 2 x − x e 2 x y^*=-\frac{1}{2}x^2e^{2x}-xe^{2x} y ∗ = − 2 1 x 2 e 2 x − x e 2 x y = y ˉ + y ∗ = c 1 e 2 x + c 2 e 3 x + ( − 1 2 x 2 − x ) e 2 x y=\bar{y}+y^*=c_1e^{2x}+c_2e^{3x}+(-\frac{1}{2}x^2-x)e^{2x} y = y ˉ + y ∗ = c 1 e 2 x + c 2 e 3 x + ( − 2 1 x 2 − x ) e 2 x
n阶常系数微分方程求解 y ( n ) + P 1 y ( n − 1 ) + … … = 0 y^{(n)}+P_1y^{(n-1)}+……=0 y ( n ) + P 1 y ( n − 1 ) + … … = 0 解法:r ( n ) + P 1 r ( n − 1 ) + … … = 0 r^{(n)}+P_1r^{(n-1)}+……=0 r ( n ) + P 1 r ( n − 1 ) + … … = 0 r 1 , r 2 , … … , r n r_1,r_2,……,r_n r 1 , r 2 , … … , r n y = c e r x y=ce^{rx} y = c e r x y = ( c 1 + c 2 x + … … + c k x k − 1 ) e r x y=(c_1+c_2x+……+c_kx^{k-1})e^{rx} y = ( c 1 + c 2 x + … … + c k x k − 1 ) e r x r = a ± b i r=a \pm bi r = a ± b i y = e a x ( c 1 cos b x + c 2 sin b x ) y=e^{ax}(c_1 \cos bx+c_2 \sin bx) y = e a x ( c 1 cos b x + c 2 sin b x ) y = e a x [ c 1 + c 2 x + … … + c k x k − 1 cos b x + ( D 1 + D 2 x + … … + D k x k − 1 ) − sin b x ] y=e^{ax}[c_1+c_2x+……+c_kx^{k-1}\cos bx+(D_1+D_2x+……+D_kx^{k-1})-\sin bx] y = e a x [ c 1 + c 2 x + … … + c k x k − 1 cos b x + ( D 1 + D 2 x + … … + D k x k − 1 ) − sin b x ] y ′ ′ ′ + 2 y ′ ′ = 0 y'''+2y''=0 y ′ ′ ′ + 2 y ′ ′ = 0 r 3 + 2 r 2 = r 2 ( r + 2 ) = 0 r^3+2r^2=r^2(r+2)=0 r 3 + 2 r 2 = r 2 ( r + 2 ) = 0 r 1 = r 2 = 0 , r 3 = − 2 r_1=r_2=0,r_3=-2 r 1 = r 2 = 0 , r 3 = − 2 r = 0 r=0 r = 0 y = ( c 2 + c 3 ) e 0 x = c 2 + c 3 x y=(c_2+c_3)e^{0x}=c_2+c_3x y = ( c 2 + c 3 ) e 0 x = c 2 + c 3 x r = − 2 r=-2 r = − 2 y = c 1 e − 2 x y=c_1e^{-2x} y = c 1 e − 2 x y = c 1 e − 2 x + c 2 + c 3 x y=c_1e^{-2x}+c_2+c_3x y = c 1 e − 2 x + c 2 + c 3 x
无穷级数 泰勒公式
常见的泰勒公式x → 0 x \to 0 x → 0 sin x = x − 1 6 x 3 + o ( x 3 ) \sin x=x-\frac{1}{6}x^3+o(x^3) sin x = x − 6 1 x 3 + o ( x 3 ) cos x = 1 − 1 2 x 2 + 1 24 x 4 + o ( x 4 ) \cos x=1-\frac{1}{2}x^2+\frac{1}{24}x^4+o(x^4) cos x = 1 − 2 1 x 2 + 2 4 1 x 4 + o ( x 4 ) tan x = x + 1 3 x 3 + o ( x 3 ) \tan x=x+\frac{1}{3}x^3+o(x^3) tan x = x + 3 1 x 3 + o ( x 3 ) arcsin x = x + 1 6 x 3 + o ( x 3 ) \arcsin x=x+\frac{1}{6}x^3+o(x^3) arcsin x = x + 6 1 x 3 + o ( x 3 ) arccos x = \arccos x= arccos x = arctan x = x − 1 3 x 3 + o ( x 3 ) \arctan x=x-\frac{1}{3}x^3+o(x^3) arctan x = x − 3 1 x 3 + o ( x 3 ) e x = 1 + x + 1 2 i x 2 + 1 3 i x 3 + o ( x 3 ) e^x=1+x+\frac{1}{2i}x^2+\frac{1}{3i}x^3+o(x^3) e x = 1 + x + 2 i 1 x 2 + 3 i 1 x 3 + o ( x 3 ) ln ( 1 + x ) = x − 1 2 x 2 + 1 3 x 3 + o ( x 3 ) \ln (1+x)=x-\frac{1}{2}x^2+\frac{1}{3}x^3+o(x^3) ln ( 1 + x ) = x − 2 1 x 2 + 3 1 x 3 + o ( x 3 ) ( 1 + x ) α = x + α x + α ( α − 1 ) 2 x 2 + o ( x 2 ) (1+x)^{\alpha }=x+\alpha x+\frac{\alpha (\alpha -1)}{2}x^2+o(x^2) ( 1 + x ) α = x + α x + 2 α ( α − 1 ) x 2 + o ( x 2 ) α = 1 2 \alpha =\frac{1}{2} α = 2 1 1 + x = 1 + 1 2 x − 1 8 x 2 + o ( x 2 ) \sqrt{1+x}=1+\frac{1}{2}x-\frac{1}{8}x^2+o(x^2) 1 + x = 1 + 2 1 x − 8 1 x 2 + o ( x 2 ) α = 1 3 \alpha =\frac{1}{3} α = 3 1 1 + x = 1 + 1 3 x − 1 9 x 2 + o ( x 2 ) \sqrt{1+x}=1+\frac{1}{3}x-\frac{1}{9}x^2+o(x^2) 1 + x = 1 + 3 1 x − 9 1 x 2 + o ( x 2 )
常用的公式x → 0 x \to 0 x → 0 tan x − sin x = 1 2 x 3 + o ( x 3 ) \tan x-\sin x=\frac{1}{2}x^3+o(x^3) tan x − sin x = 2 1 x 3 + o ( x 3 ) x − sin x = 1 6 x 3 + o ( x 3 ) x-\sin x=\frac{1}{6}x^3+o(x^3) x − sin x = 6 1 x 3 + o ( x 3 ) arcsin x − x = 1 6 x 3 + o ( x 3 ) \arcsin x -x=\frac{1}{6}x^3+o(x^3) arcsin x − x = 6 1 x 3 + o ( x 3 ) tan x − x = 1 3 x 3 + o ( x 3 ) \tan x-x=\frac{1}{3}x^3+o(x^3) tan x − x = 3 1 x 3 + o ( x 3 ) x − arctan x = 1 3 x 3 + o ( x 3 ) x-\arctan x=\frac{1}{3}x^3+o(x^3) x − arctan x = 3 1 x 3 + o ( x 3 ) tan x − sin x 1 2 x 3 \tan x-\sin x~\frac{1}{2}x^3 tan x − sin x 2 1 x 3 x − sin x 1 6 x 3 x-\sin x~\frac{1}{6}x^3 x − sin x 6 1 x 3 arcsin x − x 1 6 x 3 \arcsin x -x~\frac{1}{6}x^3 arcsin x − x 6 1 x 3 tan x − x 1 3 x 3 \tan x-x~\frac{1}{3}x^3 tan x − x 3 1 x 3 x − arctan x 1 3 x 3 x-\arctan x~\frac{1}{3}x^3 x − arctan x 3 1 x 3 x − ln ( 1 + x ) 1 2 x 2 x-\ln (1+x)~\frac{1}{2}x^2 x − ln ( 1 + x ) 2 1 x 2 e x − 1 − x 1 2 x 2 e^x-1-x~\frac{1}{2}x^2 e x − 1 − x 2 1 x 2 1 − cos α x α 2 x 2 1-\cos ^{\alpha }x~\frac{\alpha }{2}x^2 1 − cos α x 2 α x 2 f ( x ) g ( x ) − 1 g ( x ) [ f ( x ) − 1 ] f(x)^{g(x)}-1~g(x)[f(x)-1] f ( x ) g ( x ) − 1 g ( x ) [ f ( x ) − 1 ] f ( x ) → 1 f(x) \to 1 f ( x ) → 1 f ( x ) g ( x ) → 1 f(x)^{g(x)}\to 1 f ( x ) g ( x ) → 1 叶灵均的高数笔记
无穷级数的概念 将无穷多个数进行求和:记为∑ n = 1 ∞ u n = u 1 + u 2 + … + u n + … \sum_{n=1}^{\infty }u_n=u_1+u_2+…+u_n+… ∑ n = 1 ∞ u n = u 1 + u 2 + … + u n + … u n u_n u n
收敛与发散:S n = ∑ i = 1 n u i = u 1 + u 2 + … + u n S_n=\sum_{i=1}^{n}u_i=u_1+u_2+…+u_n S n = ∑ i = 1 n u i = u 1 + u 2 + … + u n lim x → ∞ S n = \lim_{x \to \infty }S_n= lim x → ∞ S n = ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑ n = 1 ∞ u n lim x → ∞ S n = ∞ \lim_{x \to \infty }S_n=\infty lim x → ∞ S n = ∞ ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑ n = 1 ∞ u n 常见数列求和 :a n = a 1 + ( n − 1 ) d a_n=a_1+(n-1)d a n = a 1 + ( n − 1 ) d S n = ( a 1 + a n ) ⋅ n 2 S_n=\frac{(a_1+a_n)\cdot n}{2} S n = 2 ( a 1 + a n ) ⋅ n a n = s 1 ⋅ q n − 1 a_n=s_1\cdot q^{n-1} a n = s 1 ⋅ q n − 1 S n = a 1 ( 1 − q n ) 1 − q ( q ≠ 1 ) S_n=\frac{a_1(1-q^n)}{1-q}(q\ne 1) S n = 1 − q a 1 ( 1 − q n ) ( q = 1 ) ∣ q ∣ < 1 , n → ∞ , q n → 0 |q|<1,n \to \infty ,q^n \to 0 ∣ q ∣ < 1 , n → ∞ , q n → 0 S n = a 1 1 − q = S_n=\frac{a_1}{1-q}= S n = 1 − q a 1 = 首项 1 − 公比 \frac{首项}{1-公比} 1 − 公 比 首 项 1 n ( n + 1 ) = 1 n − 1 n + 1 \frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1} n ( n + 1 ) 1 = n 1 − n + 1 1 ∑ n = 1 ∞ 1 n ( n + 1 ) = ∑ n = 1 ∞ ( 1 n − 1 n + 1 ) \sum_{n=1}^{\infty }\frac{1}{n(n+1)} =\sum_{n=1}^{\infty }(\frac{1}{n}-\frac{1}{n+1} ) ∑ n = 1 ∞ n ( n + 1 ) 1 = ∑ n = 1 ∞ ( n 1 − n + 1 1 ) = ( 1 − 1 2 ) + ( 1 2 − 1 3 ) + … + ( 1 n − 1 n + 1 ) =(1-\frac{1}{2} )+(\frac{1}{2}-\frac{1}{3} )+…+(\frac{1}{n}-\frac{1}{n+1}) = ( 1 − 2 1 ) + ( 2 1 − 3 1 ) + … + ( n 1 − n + 1 1 ) = 1 − 1 n + 1 = 1 =1-\frac{1}{n+1}=1 = 1 − n + 1 1 = 1
无穷级数的性质
收敛级数性质:∑ n = 1 ∞ u n \sum_{n=1}^{\infty }u_n ∑ n = 1 ∞ u n ∑ n = 1 ∞ k u n = k ∑ n = 1 ∞ u n \sum_{n=1}^{\infty }ku_n=k\sum_{n=1}^{\infty }u_n ∑ n = 1 ∞ k u n = k ∑ n = 1 ∞ u n k A kA k A 收敛 ± 收敛 = 收敛 收敛 \pm 收敛=收敛 收 敛 ± 收 敛 = 收 敛 收敛 ± 发散 = 发散 收敛 \pm 发散=发散 收 敛 ± 发 散 = 发 散 发散 ± 发散 = 不一定 发散 \pm 发散=不一定 发 散 ± 发 散 = 不 一 定 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty }u_n ∑ n = 1 ∞ u n ∑ n = 1 ∞ u n → lim n → ∞ u n = 0 \sum_{n=1}^{\infty }u_n\rightarrow \lim_{n \to \infty }u_n=0 ∑ n = 1 ∞ u n → lim n → ∞ u n = 0 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty }u_n ∑ n = 1 ∞ u n lim x → ∞ ( u n + 2 ) = ( 2 ) \lim_{x \to \infty }(u_n+2)=(2) lim x → ∞ ( u n + 2 ) = ( 2 ) u n → 0 → 0 + 2 = 2 u_n \to 0 \to 0+2=2 u n → 0 → 0 + 2 = 2
级数敛散性判别:lim x → ∞ u n ≠ 0 → ∑ n = 1 ∞ u n \lim_{x \to \infty }u_n \ne 0 \rightarrow \sum_{n=1}^{\infty }u_n lim x → ∞ u n = 0 → ∑ n = 1 ∞ u n ∑ n = 1 ∞ sin 1 n , ∑ n = 1 ∞ cos 1 n , ∑ n = 1 ∞ ( 1 + 1 n ) n , ∑ n = 1 ∞ n n \sum_{n=1}^{\infty }\sin \frac{1}{n},\sum_{n=1}^{\infty }\cos \frac{1}{n},\sum_{n=1}^{\infty }(1+\frac{1}{n})^n,\sum_{n=1}^{\infty}\sqrt[n]{n} ∑ n = 1 ∞ sin n 1 , ∑ n = 1 ∞ cos n 1 , ∑ n = 1 ∞ ( 1 + n 1 ) n , ∑ n = 1 ∞ n n n → ∞ n \to \infty n → ∞ lim n → ∞ sin 1 n \lim_{n \to \infty}\sin \frac{1}{n} lim n → ∞ sin n 1 n → ∞ , 1 n → 0 , sin 1 n 1 n n \to \infty,\frac{1}{n} \to 0,\sin \frac{1}{n}~\frac{1}{n} n → ∞ , n 1 → 0 , sin n 1 n 1 ∑ n = 1 ∞ sin 1 n = ∑ n = 1 ∞ 1 n \sum_{n=1}^{\infty}\sin \frac{1}{n}=\sum_{n=1}^{\infty }\frac{1}{n} ∑ n = 1 ∞ sin n 1 = ∑ n = 1 ∞ n 1 ∑ n = 1 ∞ 1 n \sum_{n=1}^{\infty }\frac{1}{n} ∑ n = 1 ∞ n 1 lim n → ∞ cos 1 n = 1 ≠ 0 \lim_{n \to \infty }\cos \frac{1}{n}=1 \ne 0 lim n → ∞ cos n 1 = 1 = 0 lim n → ∞ ( 1 + 1 n ) n = e ≠ 0 \lim_{n \to \infty }(1+\frac{1}{n})^n=e \ne 0 lim n → ∞ ( 1 + n 1 ) n = e = 0 lim n → ∞ n n = lim x → ∞ n 1 n = lim x → ∞ e ln x x = e lim x → ∞ 1 x = e 0 = 1 ≠ 0 \lim_{n \to \infty }\sqrt[n]{n}=\lim_{x \to \infty }n^{\frac{1}{n} }=\lim_{x \to \infty }e^{\frac{\ln x}{x} }=e^{\lim_{x \to \infty} \frac{1}{x} }=e^0=1 \ne 0 lim n → ∞ n n = lim x → ∞ n n 1 = lim x → ∞ e x l n x = e l i m x → ∞ x 1 = e 0 = 1 = 0 lim x → ∞ u n ≠ 0 \lim_{x \to \infty }u_n \ne 0 lim x → ∞ u n = 0 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty }u_n ∑ n = 1 ∞ u n ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑ n = 1 ∞ u n lim x → ∞ u n = 0 \lim_{x \to \infty}u_n=0 lim x → ∞ u n = 0
等比级数判敛方法(几何级数):∑ n = 0 ∞ a ⋅ q n \sum_{n=0}^{\infty }a\cdot q^n ∑ n = 0 ∞ a ⋅ q n ∣ q ∣ ⟹ { ∣ q ∣ < 1 , 收 ∣ q ∣ ≥ 1 , 发 |q|\Longrightarrow \left\{\begin{matrix}|q|<1 ,收\\|q| \ge 1, 发\end{matrix}\right. ∣ q ∣ ⟹ { ∣ q ∣ < 1 , 收 ∣ q ∣ ≥ 1 , 发 ∑ n = 1 ∞ 3 n \sum_{n=1}^{\infty }3^n ∑ n = 1 ∞ 3 n ∣ q ∣ = 3 > 1 |q|=3 > 1 ∣ q ∣ = 3 > 1 lim n → ∞ 3 n = ∞ ≠ 0 \lim_{n \to \infty}3^n=\infty \ne 0 lim n → ∞ 3 n = ∞ = 0 ∑ n = 1 ∞ ( − 1 ) n ⋅ 1 3 n \sum_{n=1}^{\infty }(-1)^n\cdot \frac{1}{3^n} ∑ n = 1 ∞ ( − 1 ) n ⋅ 3 n 1 lim n → ∞ ( − 1 3 ) n , ∣ q ∣ = 1 3 < 1 \lim_{n \to \infty}(\frac{-1}{3})^n,|q|=\frac{1}{3} < 1 lim n → ∞ ( 3 − 1 ) n , ∣ q ∣ = 3 1 < 1 ∑ n = 1 ∞ ( 1 4 ) n ⋅ 1 n \sum_{n=1}^{\infty }(\frac{1}{4})^n\cdot \frac{1}{n} ∑ n = 1 ∞ ( 4 1 ) n ⋅ n 1 lim n → ∞ ( 1 4 ) n , ∣ q ∣ = 1 4 < 1 \lim_{n \to \infty}(\frac{1}{4})^n,|q| =\frac{1}{4} <1 lim n → ∞ ( 4 1 ) n , ∣ q ∣ = 4 1 < 1 ∑ n = 1 ∞ ( − 1 ) n − 1 ⋅ 2 n 3 n \sum_{n=1}^{\infty }(-1)^{n-1}\cdot \frac{2^n}{3^n} ∑ n = 1 ∞ ( − 1 ) n − 1 ⋅ 3 n 2 n − lim n → ∞ ( − 2 3 ) n , ∣ q ∣ = 2 3 < 1 -\lim_{n \to \infty}(-\frac{2}{3})^n,|q|=\frac{2}{3}<1 − lim n → ∞ ( − 3 2 ) n , ∣ q ∣ = 3 2 < 1 ∑ n = 1 ∞ 2 n − 1 3 n \sum_{n=1}^{\infty }\frac{2^n-1}{3^n} ∑ n = 1 ∞ 3 n 2 n − 1 ∑ n = 0 ∞ 2 n 3 n − ∑ n = 1 ∞ ( 1 3 ) n , ∣ q 1 ∣ = 2 3 < 1 , ∣ q 2 ∣ = 1 3 < 1 \sum_{n=0}^{\infty }\frac{2^n}{3^n}-\sum_{n=1}^{\infty}(\frac{1}{3})^n,|q_1|=\frac{2}{3}<1,|q_2|=\frac{1}{3}<1 ∑ n = 0 ∞ 3 n 2 n − ∑ n = 1 ∞ ( 3 1 ) n , ∣ q 1 ∣ = 3 2 < 1 , ∣ q 2 ∣ = 3 1 < 1 收敛 ± 收敛 = 收敛 收敛\pm 收敛=收敛 收 敛 ± 收 敛 = 收 敛 ∑ n = 1 ∞ ( 3 2 ) n \sum_{n=1}^{\infty }(\frac{3}{2})^n ∑ n = 1 ∞ ( 2 3 ) n lim n → ∞ ( 3 2 ) n , ∣ q ∣ = 3 2 > 1 \lim_{n \to \infty}(\frac{3}{2})^n,|q|=\frac{3}{2}>1 lim n → ∞ ( 2 3 ) n , ∣ q ∣ = 2 3 > 1
P级数判别法:∑ n = 1 ∞ 1 n P \sum_{n=1}^{\infty }\frac{1}{n^P} ∑ n = 1 ∞ n P 1 P > 0 P>0 P > 0 p ⟹ { p > 1 , 收 p ≤ 1 , 发 p\Longrightarrow \left\{\begin{matrix}p>1 ,收\\p \le 1, 发\end{matrix}\right. p ⟹ { p > 1 , 收 p ≤ 1 , 发 ∑ n = 1 ∞ 1 n 1 , P = 1 \sum_{n=1}^{\infty }\frac{1}{n^1},P=1 ∑ n = 1 ∞ n 1 1 , P = 1 ∑ n = 1 ∞ 1 n 2 4 \sum_{n=1}^{\infty }\frac{1}{\sqrt[4]{n^2} } ∑ n = 1 ∞ 4 n 2 1 ∑ n = 1 ∞ 1 n 2 4 = ∑ n = 1 ∞ 1 n 1 2 \sum_{n=1}^{\infty }\frac{1}{\sqrt[4]{n^2} }=\sum_{n=1}^{\infty }\frac{1}{n^{\frac{1}{2} } } ∑ n = 1 ∞ 4 n 2 1 = ∑ n = 1 ∞ n 2 1 1 P = 1 2 < 1 P=\frac{1}{2} <1 P = 2 1 < 1
正项级数判别法:∑ n = 1 ∞ u n ( u n > 0 ) \sum_{n=1}^{\infty }u_n(u_n > 0) ∑ n = 1 ∞ u n ( u n > 0 ) u n u_n u n lim n → ∞ u n + 1 u n ⟹ { < 1 , 收 > 1 , 发 = 1 ,失效 \lim_{n \to \infty} \frac{u_n+1}{u_n}\Longrightarrow \left\{\begin{matrix}<1,收\\>1,发\\=1,失效\end{matrix}\right. lim n → ∞ u n u n + 1 ⟹ ⎩ ⎪ ⎨ ⎪ ⎧ < 1 , 收 > 1 , 发 = 1 , 失 效 u n u_n u n n ! , a n , n n n!,a^n,n^n n ! , a n , n n ∑ n = 1 ∞ 2 n n ! \sum_{n=1}^{\infty }\frac{2^n}{n!} ∑ n = 1 ∞ n ! 2 n u n = 2 n n ! , u n + 1 = 2 n + 1 ( n + 1 ) ! u_n=\frac{2^n}{n!},u_{n+1}=\frac{2^{n+1} }{(n+1)!} u n = n ! 2 n , u n + 1 = ( n + 1 ) ! 2 n + 1 lim n → ∞ u n + 1 u n = lim n → ∞ 2 n + 1 ⋅ n ! 2 n ⋅ ( n + 1 ) ! \lim_{n \to \infty}\frac{u_{n+1} }{u_n}=\lim_{n \to \infty}\frac{2^{n+1} \cdot n!}{2^n \cdot (n+1)!} lim n → ∞ u n u n + 1 = lim n → ∞ 2 n ⋅ ( n + 1 ) ! 2 n + 1 ⋅ n ! = lim n → ∞ 2 ⋅ n ! n ! ⋅ ( n + 1 ) ! =\lim_{n \to \infty}2 \cdot \frac{n!}{n!\cdot (n+1)!} = lim n → ∞ 2 ⋅ n ! ⋅ ( n + 1 ) ! n ! = lim n → ∞ 2 ( n + 1 ) =\lim_{n \to \infty}\frac{2}{(n+1)} = lim n → ∞ ( n + 1 ) 2 = 0 < 1 =0<1 = 0 < 1 ∑ n = 1 ∞ 2 n ⋅ n ! n n \sum_{n=1}^{\infty }\frac{2^n\cdot n!}{n^n} ∑ n = 1 ∞ n n 2 n ⋅ n ! u n = 2 n ⋅ n ! n n , u n + 1 = 2 n + 1 ⋅ ( n + 1 ) ! ( n + 1 ) n + 1 u_n=\frac{2^n\cdot n!}{n^n},u_{n+1}=\frac{2^{n+1} \cdot (n+1)!}{(n+1)^{n+1} } u n = n n 2 n ⋅ n ! , u n + 1 = ( n + 1 ) n + 1 2 n + 1 ⋅ ( n + 1 ) ! lim n → ∞ u n + 1 u n = lim n → ∞ 2 n + 1 ⋅ ( n + 1 ) ! ⋅ n ! 2 n ⋅ n ! ⋅ ( n + 1 ) n + 1 \lim_{n \to \infty}\frac{u_{n+1} }{u_n}=\lim_{n \to \infty}\frac{2^{n+1} \cdot (n+1)! \cdot n!}{2^n \cdot n! \cdot (n+1)^{n+1} } lim n → ∞ u n u n + 1 = lim n → ∞ 2 n ⋅ n ! ⋅ ( n + 1 ) n + 1 2 n + 1 ⋅ ( n + 1 ) ! ⋅ n ! = lim n → ∞ 2 n + 1 2 n ⋅ ( n + 1 ) ! n ! ⋅ n n ( n + 1 ) n + 1 =\lim_{n \to \infty}\frac{2^{n+1} }{2^n}\cdot \frac{(n+1)!}{n!}\cdot \frac{n^n}{(n+1)^{n+1}} = lim n → ∞ 2 n 2 n + 1 ⋅ n ! ( n + 1 ) ! ⋅ ( n + 1 ) n + 1 n n = lim n → ∞ 2 ( n + 1 ) ⋅ n n ( n + 1 ) n + 1 =\lim_{n \to \infty}2(n+1)\cdot \frac{n^n}{(n+1)^{n+1}} = lim n → ∞ 2 ( n + 1 ) ⋅ ( n + 1 ) n + 1 n n = lim n → ∞ 2 ⋅ ( n ( n + 1 ) ) n =\lim_{n \to \infty}2\cdot (\frac{n}{(n+1)})^n = lim n → ∞ 2 ⋅ ( ( n + 1 ) n ) n = lim n → ∞ 2 ⋅ e − n n + 1 =\lim_{n \to \infty}2\cdot e^{\frac{-n}{n+1}} = lim n → ∞ 2 ⋅ e n + 1 − n = 2 ⋅ e − 1 = 2 e < 1 =2 \cdot e^{-1}=\frac{2}{e}<1 = 2 ⋅ e − 1 = e 2 < 1 ∑ n = 1 ∞ v n \sum_{n=1}^{\infty }v_n ∑ n = 1 ∞ v n lim n → ∞ u n v n = A \lim_{n \to \infty}\frac{u_n}{v_n}=A lim n → ∞ v n u n = A A { A 为常数,同敛散性 0 ,大收小收 ∞ , 小发大发 A\left\{\begin{matrix}A为常数,同敛散性\\0,大收小收\\\infty,小发大发\end{matrix}\right. A ⎩ ⎪ ⎨ ⎪ ⎧ A 为 常 数 , 同 敛 散 性 0 , 大 收 小 收 ∞ , 小 发 大 发 n → ∞ n \to \infty n → ∞ u n v n u_n~v_n u n v n u n , v n u_n,v_n u n , v n ∑ n = 1 ∞ u n \sum_{n=1}^{\infty }u_n ∑ n = 1 ∞ u n ∑ n = 1 ∞ v n \sum_{n=1}^{\infty }v_n ∑ n = 1 ∞ v n ∑ n = 0 ∞ sin ( 1 2 n ) \sum_{n=0}^{\infty }\sin (\frac{1}{2^n}) ∑ n = 0 ∞ sin ( 2 n 1 ) n → ∞ , 1 2 n → 0 sin 1 2 n 1 2 n n \to \infty,\frac{1}{2^n}\to 0 \sin \frac{1}{2^n}~\frac{1}{2^n} n → ∞ , 2 n 1 → 0 sin 2 n 1 2 n 1 ∑ n = 0 ∞ sin ( 1 2 n ) 与 ∑ n = 0 ∞ 1 2 n \sum_{n=0}^{\infty}\sin (\frac{1}{2^n})与\sum_{n=0}^{\infty}\frac{1}{2^n} ∑ n = 0 ∞ sin ( 2 n 1 ) 与 ∑ n = 0 ∞ 2 n 1 ∑ n = 0 ∞ 1 n 2 n = ∑ n = 0 ∞ ( 1 2 ) n ; ∣ q ∣ = 1 2 < 1 \sum_{n=0}^{\infty}\frac{1^n}{2^n}=\sum_{n=0}^{\infty}(\frac{1}{2})^n;|q|=\frac{1}{2}<1 ∑ n = 0 ∞ 2 n 1 n = ∑ n = 0 ∞ ( 2 1 ) n ; ∣ q ∣ = 2 1 < 1 ∑ n = 0 ∞ sin ( 1 2 n ) \sum_{n=0}^{\infty}\sin (\frac{1}{2^n}) ∑ n = 0 ∞ sin ( 2 n 1 ) ∑ n = 1 ∞ ln ( 1 + 1 n ) \sum_{n=1}^{\infty }\ln (1+\frac{1}{n}) ∑ n = 1 ∞ ln ( 1 + n 1 ) n → ∞ , 1 n → 0 , ln ( 1 + 1 n ) 1 2 n n \to \infty,\frac{1}{n}\to 0 ,\ln (1+\frac{1}{n})~\frac{1}{2^n} n → ∞ , n 1 → 0 , ln ( 1 + n 1 ) 2 n 1 ∑ n = 1 ∞ ln ( 1 + 1 n ) 与 ∑ n = 1 ∞ 1 n \sum_{n=1}^{\infty}\ln (1+\frac{1}{n})与\sum_{n=1}^{\infty}\frac{1}{n} ∑ n = 1 ∞ ln ( 1 + n 1 ) 与 ∑ n = 1 ∞ n 1 ∑ n = 1 ∞ 1 n = ∑ n = 0 ∞ 1 n 1 ; P = 1 \sum_{n=1}^{\infty}\frac{1}{n}=\sum_{n=0}^{\infty}\frac{1}{n^1};P=1 ∑ n = 1 ∞ n 1 = ∑ n = 0 ∞ n 1 1 ; P = 1 ∑ n = 1 ∞ ln ( 1 + 1 n ) \sum_{n=1}^{\infty}\ln (1+\frac{1}{n}) ∑ n = 1 ∞ ln ( 1 + n 1 ) ∑ n = 1 ∞ 1 n ⋅ ln ( 1 + 1 n ) \sum_{n=1}^{\infty }\frac{1}{\sqrt{n} }\cdot \ln (1+\frac{1}{n}) ∑ n = 1 ∞ n 1 ⋅ ln ( 1 + n 1 ) n → ∞ , 1 n → 0 , ln ( 1 + 1 n ) 1 2 n n \to \infty,\frac{1}{n}\to 0 ,\ln (1+\frac{1}{n})~\frac{1}{2^n} n → ∞ , n 1 → 0 , ln ( 1 + n 1 ) 2 n 1 ∑ n = 1 ∞ ln ( 1 + 1 n ) 与 ∑ n = 1 ∞ 1 n ⋅ n n \sum_{n=1}^{\infty}\ln (1+\frac{1}{n})与\sum_{n=1}^{\infty}\frac{1}{n\cdot \sqrt[n]{n} } ∑ n = 1 ∞ ln ( 1 + n 1 ) 与 ∑ n = 1 ∞ n ⋅ n n 1 ∑ n = 1 ∞ 1 n ⋅ n n = ∑ n = 0 ∞ ( 1 n 3 2 ; P = 3 2 \sum_{n=1}^{\infty}\frac{1}{n\cdot \sqrt[n]{n} }=\sum_{n=0}^{\infty}(\frac{1}{n^{\frac{3}{2} } };P=\frac{3}{2} ∑ n = 1 ∞ n ⋅ n n 1 = ∑ n = 0 ∞ ( n 2 3 1 ; P = 2 3 ∑ n = 1 ∞ ln ( 1 + 1 n ) \sum_{n=1}^{\infty}\ln (1+\frac{1}{n}) ∑ n = 1 ∞ ln ( 1 + n 1 ) ∑ n = 1 ∞ 1 n ⋅ n n \sum_{n=1}^{\infty }\frac{1}{n \cdot \sqrt[n]{n} } ∑ n = 1 ∞ n ⋅ n n 1 n → ∞ , n n = 1 , 1 n → 0 , 1 n ⋅ n n ) 1 n n \to \infty,\sqrt[n]{n}=1,\frac{1}{n}\to 0 ,\frac{1}{n\cdot \sqrt[n]{n} } )~\frac{1}{n} n → ∞ , n n = 1 , n 1 → 0 , n ⋅ n n 1 ) n 1 ∑ n = 1 ∞ 1 n ⋅ n n 与 ∑ n = 1 ∞ 1 n \sum_{n=1}^{\infty}\frac{1}{n\cdot \sqrt[n]{n}}与\sum_{n=1}^{\infty}\frac{1}{n} ∑ n = 1 ∞ n ⋅ n n 1 与 ∑ n = 1 ∞ n 1 ∑ n = 1 ∞ 1 n = ∑ n = 1 ∞ 1 n 1 ; P = 1 \sum_{n=1}^{\infty}\frac{1}{n}=\sum_{n=1}^{\infty}\frac{1}{n^1};P=1 ∑ n = 1 ∞ n 1 = ∑ n = 1 ∞ n 1 1 ; P = 1 ∑ n = 1 ∞ 1 n ⋅ n n \sum_{n=1}^{\infty}\frac{1}{n\cdot \sqrt[n]{n} } ∑ n = 1 ∞ n ⋅ n n 1 ∑ n = 1 ∞ 2 n ⋅ sin π 3 n \sum_{n=1}^{\infty }2^n\cdot \sin \frac{\pi}{3^n} ∑ n = 1 ∞ 2 n ⋅ sin 3 n π n → ∞ , π 3 n → 0 , sin π 3 n π 3 n n \to \infty,\frac{\pi }{3^n}\to 0 ,\sin \frac{\pi }{3^n}~\frac{\pi }{3^n} n → ∞ , 3 n π → 0 , sin 3 n π 3 n π ∑ n = 1 ∞ 2 n ⋅ sin π 3 n 与 π ∑ n = 1 ∞ 2 n ⋅ 1 3 n \sum_{n=1}^{\infty}2^n \cdot \sin \frac{\pi }{3^n}与\pi \sum_{n=1}^{\infty}2^n\cdot \frac{1}{3^n} ∑ n = 1 ∞ 2 n ⋅ sin 3 n π 与 π ∑ n = 1 ∞ 2 n ⋅ 3 n 1 π ∑ n = 1 ∞ 2 n 3 n = ∑ n = 0 ∞ ( 2 3 ) n ; ∣ q ∣ = 2 3 < 1 \pi \sum_{n=1}^{\infty}\frac{2^n}{3^n}=\sum_{n=0}^{\infty}(\frac{2}{3})^n;|q|=\frac{2}{3}<1 π ∑ n = 1 ∞ 3 n 2 n = ∑ n = 0 ∞ ( 3 2 ) n ; ∣ q ∣ = 3 2 < 1 ∑ n = 1 ∞ ln ( 1 + 1 n ) \sum_{n=1}^{\infty}\ln (1+\frac{1}{n}) ∑ n = 1 ∞ ln ( 1 + n 1 ) ∑ n = 1 ∞ n + 1 − n − 1 n \sum_{n=1}^{\infty }\frac{\sqrt{n+1}-\sqrt{n-1} }{n} ∑ n = 1 ∞ n n + 1 − n − 1 ( n + 1 − n − 1 ) ( n + 1 + n − 1 ) n ⋅ ( n + 1 + n − 1 ) = 2 n ( n + 1 + n − 1 ) \frac{(\sqrt{n+1}-\sqrt{n-1})(\sqrt{n+1}+\sqrt{n-1}) }{n\cdot (\sqrt{n+1}+\sqrt{n-1}) }=\frac{2}{n(\sqrt{n+1}+\sqrt{n-1} ) } n ⋅ ( n + 1 + n − 1 ) ( n + 1 − n − 1 ) ( n + 1 + n − 1 ) = n ( n + 1 + n − 1 ) 2 2 n ⋅ 2 n 1 n ⋅ n ~\frac{2}{n\cdot 2\sqrt{n} }~\frac{1}{n \cdot \sqrt{n} } n ⋅ 2 n 2 n ⋅ n 1 n → ∞ , n + 1 − n − 1 n 1 n ⋅ n n \to \infty,\frac{\sqrt{n+1}-\sqrt{n-1} }{n}~\frac{1}{n\cdot \sqrt{n} } n → ∞ , n n + 1 − n − 1 n ⋅ n 1 ∑ n = 1 ∞ n + 1 − n − 1 n 与 ∑ n = 1 ∞ 1 n ⋅ n \sum_{n=1}^{\infty}\frac{\sqrt{n+1}-\sqrt{n-1} }{n}与\sum_{n=1}^{\infty}\frac{1}{n\cdot \sqrt{n} } ∑ n = 1 ∞ n n + 1 − n − 1 与 ∑ n = 1 ∞ n ⋅ n 1 ∑ n = 0 ∞ 1 n 1 ⋅ n 1 2 = ∑ n = 1 ∞ 1 n 3 2 ; P = 3 2 > 1 \sum_{n=0}^{\infty}\frac{1}{n^1\cdot n^{\frac{1}{2} } }=\sum_{n=1}^{\infty}\frac{1}{n^{\frac{3}{2} } };P=\frac{3}{2}>1 ∑ n = 0 ∞ n 1 ⋅ n 2 1 1 = ∑ n = 1 ∞ n 2 3 1 ; P = 2 3 > 1 ∑ n = 1 ∞ ln ( 1 + 1 n ) \sum_{n=1}^{\infty}\ln (1+\frac{1}{n}) ∑ n = 1 ∞ ln ( 1 + n 1 ) n → ∞ , n n = 1 {\color{Red} n \to \infty ,\sqrt[n]{n}=1 } n → ∞ , n n = 1 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty }u_n ∑ n = 1 ∞ u n u n u_n u n n a n^a n a a n a^n a n ∑ n = 1 ∞ v n \sum_{n=1}^{\infty}v_n ∑ n = 1 ∞ v n ∑ n = 1 ∞ n + 1 n ( n + 2 ) \sum_{n=1}^{\infty }\frac{n+1}{n(n+2)} ∑ n = 1 ∞ n ( n + 2 ) n + 1 ∑ n = 1 ∞ v n = ∑ n = 1 ∞ 1 n \sum_{n=1}^{\infty}v_n=\sum_{n=1}^{\infty}\frac{1}{n} ∑ n = 1 ∞ v n = ∑ n = 1 ∞ n 1 lim n → ∞ u n v n = lim n → ∞ ( n + 1 ) ⋅ n n ( n + 2 ) = 1 \lim_{n \to \infty }\frac{u_n}{v_n}=\lim_{n \to \infty}\frac{(n+1)\cdot n}{n(n+2)}=1 lim n → ∞ v n u n = lim n → ∞ n ( n + 2 ) ( n + 1 ) ⋅ n = 1 ∑ n = 1 ∞ 1 n \sum_{n=1}^{\infty}\frac{1}{n} ∑ n = 1 ∞ n 1 ∑ n = 1 ∞ n + 1 n ( n + 2 ) \sum_{n=1}^{\infty}\frac{n+1}{n(n+2)} ∑ n = 1 ∞ n ( n + 2 ) n + 1 ∑ n = 1 ∞ 1 n \sum_{n=1}^{\infty}\frac{1}{n} ∑ n = 1 ∞ n 1 ∑ n = 1 ∞ 1 2 n + 4 \sum_{n=1}^{\infty }\frac{1}{2^n+4} ∑ n = 1 ∞ 2 n + 4 1 ∑ n = 1 ∞ v n = ∑ n = 1 ∞ 1 2 n \sum_{n=1}^{\infty}v_n=\sum_{n=1}^{\infty}\frac{1}{2^n} ∑ n = 1 ∞ v n = ∑ n = 1 ∞ 2 n 1 lim n → ∞ u n v n = lim n → ∞ 2 n 2 n + 4 = 1 \lim_{n \to \infty }\frac{u_n}{v_n}=\lim_{n \to \infty}\frac{2^n}{2^n+4}=1 lim n → ∞ v n u n = lim n → ∞ 2 n + 4 2 n = 1 ∑ n = 1 ∞ 1 2 n \sum_{n=1}^{\infty}\frac{1}{2^n} ∑ n = 1 ∞ 2 n 1 ∑ n = 1 ∞ 1 2 n + 4 \sum_{n=1}^{\infty}\frac{1}{2^n+4} ∑ n = 1 ∞ 2 n + 4 1 ∑ n = 1 ∞ 1 2 n = ∑ n = 1 ∞ ( 1 2 ) n , ∣ q ∣ = 1 2 < 1 \sum_{n=1}^{\infty}\frac{1}{2^n}=\sum_{n=1}^{\infty}(\frac{1}{2})^n,|q|=\frac{1}{2}<1 ∑ n = 1 ∞ 2 n 1 = ∑ n = 1 ∞ ( 2 1 ) n , ∣ q ∣ = 2 1 < 1 ∑ n = 1 ∞ 1 4 n 3 + 5 \sum_{n=1}^{\infty }\frac{1}{\sqrt{4n^3+5} } ∑ n = 1 ∞ 4 n 3 + 5 1 ∑ n = 1 ∞ v n = ∑ n = 1 ∞ 1 2 n 3 2 = 1 2 ∑ n = 1 ∞ 1 n 3 2 \sum_{n=1}^{\infty}v_n=\sum_{n=1}^{\infty}\frac{1}{2n^{\frac{3}{2} } }=\frac{1}{2}\sum_{n=1}^{\infty}\frac{1}{n^{\frac{3}{2} } } ∑ n = 1 ∞ v n = ∑ n = 1 ∞ 2 n 2 3 1 = 2 1 ∑ n = 1 ∞ n 2 3 1 1 2 ∑ n = 1 ∞ 1 n 3 2 \frac{1}{2}\sum_{n=1}^{\infty}\frac{1}{n^{\frac{3}{2} } } 2 1 ∑ n = 1 ∞ n 2 3 1 ∑ n = 1 ∞ 1 4 n 3 + 5 \sum_{n=1}^{\infty}\frac{1}{\sqrt{4n^3+5} } ∑ n = 1 ∞ 4 n 3 + 5 1 1 2 ∑ n = 1 ∞ 1 n 3 2 , P = 3 2 > 1 \frac{1}{2}\sum_{n=1}^{\infty}\frac{1}{n^{\frac{3}{2} } },P=\frac{3}{2}>1 2 1 ∑ n = 1 ∞ n 2 3 1 , P = 2 3 > 1 ∑ n = 1 ∞ ( 1 n + 1 − 1 n ⋅ n ) \sum_{n=1}^{\infty }(\frac{1}{\sqrt{n+1} }-\frac{1}{n \cdot \sqrt{n} } ) ∑ n = 1 ∞ ( n + 1 1 − n ⋅ n 1 ) ∑ n = 1 ∞ 1 n + 1 − ∑ n = 1 ∞ 1 n ⋅ n \sum_{n=1}^{\infty}\frac{1}{\sqrt{n+1} }-\sum_{n=1}^{\infty}\frac{1}{n \cdot \sqrt{n} } ∑ n = 1 ∞ n + 1 1 − ∑ n = 1 ∞ n ⋅ n 1 ∑ n = 1 ∞ 1 n + 1 ∑ n = 1 ∞ 1 n ; ∑ n = 1 ∞ 1 n ⋅ n ∑ n = 1 ∞ 1 n 3 2 \sum_{n=1}^{\infty}\frac{1}{\sqrt{n+1} }~\sum_{n=1}^{\infty}\frac{1}{\sqrt{n} };\sum_{n=1}^{\infty}\frac{1}{n \cdot \sqrt{n} }~\sum_{n=1}^{\infty}\frac{1}{\sqrt{n^{\frac{3}{2} } } } ∑ n = 1 ∞ n + 1 1 ∑ n = 1 ∞ n 1 ; ∑ n = 1 ∞ n ⋅ n 1 ∑ n = 1 ∞ n 2 3 1 ∑ n = 1 ∞ 1 n 1 2 , P = 1 2 < 1 ; ∑ n = 1 ∞ 1 n 3 2 , P = 3 2 > 1 \sum_{n=1}^{\infty}\frac{1}{n^{\frac{1}{2}} },P=\frac{1}{2}<1;\sum_{n=1}^{\infty}\frac{1}{\sqrt{n^{\frac{3}{2} } } },P=\frac{3}{2}>1 ∑ n = 1 ∞ n 2 1 1 , P = 2 1 < 1 ; ∑ n = 1 ∞ n 2 3 1 , P = 2 3 > 1 sin ∞ , cos ∞ , ( − 1 ) ∞ ≤ 1 \sin \infty,\cos \infty,(-1)^{\infty} \le 1 sin ∞ , cos ∞ , ( − 1 ) ∞ ≤ 1 n → ∞ n \to \infty n → ∞ u n u_n u n sin ∞ cos ∞ ≤ 1 \sin \infty \cos \infty \le 1 sin ∞ cos ∞ ≤ 1 a 2 + b 2 ≥ 2 a b ; a + b ≥ 2 a b a^2+b^2 \ge 2ab; a+b \ge 2\sqrt{ab} a 2 + b 2 ≥ 2 a b ; a + b ≥ 2 a b ∑ n = 1 ∞ sin n x n 2 \sum_{n=1}^{\infty }\frac{\sin nx}{n^2} ∑ n = 1 ∞ n 2 s i n n x n → ∞ n \to \infty n → ∞ sin n x n 2 ≤ 1 n 2 \frac{\sin nx}{n^2} \le \frac{1}{n^2} n 2 s i n n x ≤ n 2 1 sin n x n 2 ≤ 1 n 2 \frac{\sin nx}{n^2} \le \frac{1}{n^2} n 2 s i n n x ≤ n 2 1 ∑ n = 1 ∞ 1 n 2 , P = 2 > 1 \sum_{n=1}^{\infty}\frac{1}{n^2},P=2>1 ∑ n = 1 ∞ n 2 1 , P = 2 > 1 ∑ n = 1 ∞ sin n x n 2 \sum_{n=1}^{\infty }\frac{\sin nx}{n^2} ∑ n = 1 ∞ n 2 s i n n x ∑ n = 1 ∞ b n \sum_{n=1}^{\infty }bn ∑ n = 1 ∞ b n ∑ n = 1 ∞ a n 2 \sum_{n=1}^{\infty }a_n^2 ∑ n = 1 ∞ a n 2 ∑ n = 1 ∞ ∣ a + n ∣ n 2 + b n = ( ) \sum_{n=1}^{\infty}\frac{|a_+n|}{\sqrt{n^2+bn} }=() ∑ n = 1 ∞ n 2 + b n ∣ a + n ∣ = ( ) ∣ a n ∣ n 2 + b n ≤ ∣ a n ∣ n ≤ 1 2 ( a n 2 + 1 n 2 ) \frac{|a_n|}{\sqrt{n^2+bn} }\le \frac{|a_n|}{n} \le \frac{1}{2}(a_n^2+\frac{1}{n^2}) n 2 + b n ∣ a n ∣ ≤ n ∣ a n ∣ ≤ 2 1 ( a n 2 + n 2 1 ) ∑ n = 1 ∞ 1 2 ( a n 2 + 1 n 2 ) \sum_{n=1}^{\infty} \frac{1}{2}(a_n^2+\frac{1}{n^2}) ∑ n = 1 ∞ 2 1 ( a n 2 + n 2 1 )
交错级数及敛散性判别法 定义:称∑ n = 1 ∞ ( − 1 ) n ⋅ u n \sum_{n=1}^{\infty}(-1)^n\cdot u_n ∑ n = 1 ∞ ( − 1 ) n ⋅ u n ∑ n = 1 ∞ ( − 1 ) n − 1 ⋅ u n \sum_{n=1}^{\infty}(-1)^{n-1}\cdot u_n ∑ n = 1 ∞ ( − 1 ) n − 1 ⋅ u n u n u_n u n ∑ n = 1 ∞ ( − 1 ) n u n \sum_{n=1}^{\infty}(-1)^nu_n ∑ n = 1 ∞ ( − 1 ) n u n { lim n → ∞ u n = 0 u n ≥ u n + 1 } → \begin{Bmatrix}\lim_{n \to \infty}u_n=0 \\u_n \ge u_{n+1}\end{Bmatrix}\to { lim n → ∞ u n = 0 u n ≥ u n + 1 } → ∑ n = 1 ∞ ( − 1 ) n ⋅ u n \sum_{n=1}^{\infty}(-1)^n \cdot u_n ∑ n = 1 ∞ ( − 1 ) n ⋅ u n lim n → ∞ u n ≠ 0 \lim_{n \to \infty}u_n \ne 0 lim n → ∞ u n = 0 u n ≥ u n + 1 u_n \ge u_{n+1} u n ≥ u n + 1 u n − u n + 1 ≥ 0 ; u n + 1 u n ≤ 1 ; u n u_n-u_{n+1} \ge 0;\frac{u_{n+1} }{u_n}\le 1;u_n u n − u n + 1 ≥ 0 ; u n u n + 1 ≤ 1 ; u n lim n → ∞ u n = 0 \lim_{n \to \infty}u_n=0 lim n → ∞ u n = 0 u n u_n u n 不能直接求导,需要把n改为x后再求导 ;∑ n = 1 ∞ ( − 1 ) n ⋅ 1 n ! \sum_{n=1}^{\infty}(-1)^n\cdot \frac{1}{n!} ∑ n = 1 ∞ ( − 1 ) n ⋅ n ! 1 u n = 1 n ! , u n + 1 = 1 ( n + 1 ) ! u_n=\frac{1}{n!},u_{n+1}=\frac{1}{(n+1)!} u n = n ! 1 , u n + 1 = ( n + 1 ) ! 1 lim n → ∞ u n = lim n → ∞ 1 n ! = 0 \lim_{n \to \infty}u_n=\lim_{n \to \infty}\frac{1}{n!}=0 lim n → ∞ u n = lim n → ∞ n ! 1 = 0 u n > u n + 1 u_n> u_{n+1} u n > u n + 1 ∑ n = 1 ∞ ( − 1 ) n ⋅ 1 n ! \sum_{n=1}^{\infty}(-1)^n \cdot \frac{1}{n!} ∑ n = 1 ∞ ( − 1 ) n ⋅ n ! 1 ∑ n = 0 ∞ ( − 1 ) n ⋅ 1 n 2 \sum_{n=0}^{\infty}(-1)^n\cdot \frac{1}{n^2} ∑ n = 0 ∞ ( − 1 ) n ⋅ n 2 1 u n = 1 n 2 , u n + 1 = 1 ( n + 1 ) 2 u_n=\frac{1}{n^2},u_{n+1}=\frac{1}{(n+1)^2} u n = n 2 1 , u n + 1 = ( n + 1 ) 2 1 lim n → ∞ u n = lim n → ∞ 1 n 2 = 0 \lim_{n \to \infty}u_n=\lim_{n \to \infty}\frac{1}{n^2}=0 lim n → ∞ u n = lim n → ∞ n 2 1 = 0 u n > u n + 1 u_n> u_{n+1} u n > u n + 1 ∑ n = 1 ∞ ( − 1 ) n ⋅ 1 n 2 \sum_{n=1}^{\infty}(-1)^n \cdot \frac{1}{n^2} ∑ n = 1 ∞ ( − 1 ) n ⋅ n 2 1 ∑ n = 1 ∞ ( − 1 ) n − 1 ⋅ n 3 n − 1 \sum_{n=1}^{\infty}(-1)^{n-1}\cdot \frac{n}{3^{n-1} } ∑ n = 1 ∞ ( − 1 ) n − 1 ⋅ 3 n − 1 n u n = n 3 n − 1 , u n + 1 = n + 1 3 n u_n=\frac{n}{3^{n-1} },u_{n+1}=\frac{n+1}{3^n} u n = 3 n − 1 n , u n + 1 = 3 n n + 1 lim x → ∞ u x = lim n → ∞ x 3 x − 1 = lim x → ∞ 1 3 x − 1 ⋅ ln 3 = 0 \lim_{x \to \infty}u_x=\lim_{n \to \infty}\frac{x}{3^{x-1} }=\lim_{x \to \infty}\frac{1}{3^{x-1}\cdot \ln 3}=0 lim x → ∞ u x = lim n → ∞ 3 x − 1 x = lim x → ∞ 3 x − 1 ⋅ l n 3 1 = 0 f ( x ) = x 3 x − 1 , f ′ ( x ) = 3 x − 1 − x ⋅ 3 x − 1 ⋅ ln 3 ( 3 x − 1 ) 2 f(x)=\frac{x}{3^{x-1} },f'(x)=\frac{3^{x-1}-x \cdot 3^{x-1}\cdot \ln 3}{(3^{x-1})^2} f ( x ) = 3 x − 1 x , f ′ ( x ) = ( 3 x − 1 ) 2 3 x − 1 − x ⋅ 3 x − 1 ⋅ l n 3 = 3 x − 1 ( 1 − x ⋅ ln 3 ) ( 3 x − 1 ) 2 = 1 − x ln 3 3 x − 1 =\frac{3^{x-1}(1-x \cdot \ln 3)}{(3^{x-1})^2}=\frac{1-x\ln 3}{3^{x-1} } = ( 3 x − 1 ) 2 3 x − 1 ( 1 − x ⋅ l n 3 ) = 3 x − 1 1 − x l n 3 x → ∞ x \to \infty x → ∞ f ′ ( x ) < 0 , f'(x)<0, f ′ ( x ) < 0 , u n u_n u n ∑ n = 1 ∞ ( − 1 ) n − 1 ⋅ n 3 n − 1 \sum_{n=1}^{\infty}(-1)^{n-1}\cdot \frac{n}{3^{n-1} } ∑ n = 1 ∞ ( − 1 ) n − 1 ⋅ 3 n − 1 n ∑ n = 1 ∞ ( − 1 ) n ⋅ n n + 1 \sum_{n=1}^{\infty}(-1)^n\cdot \frac{n}{n+1} ∑ n = 1 ∞ ( − 1 ) n ⋅ n + 1 n u n = n n + 1 , u n + 1 = n + 1 n + 2 u_n=\frac{n}{n+1},u_{n+1}=\frac{n+1}{n+2} u n = n + 1 n , u n + 1 = n + 2 n + 1 lim n → ∞ u n = lim n → ∞ n n + 1 = 1 ≠ 0 \lim_{n \to \infty}u_n=\lim_{n \to \infty}\frac{n}{n+1}=1\ne 0 lim n → ∞ u n = lim n → ∞ n + 1 n = 1 = 0 s u m n = 1 ∞ ( − 1 ) n − 1 ⋅ n 3 n − 1 sum_{n=1}^{\infty}(-1)^{n-1}\cdot \frac{n}{3^{n-1} } s u m n = 1 ∞ ( − 1 ) n − 1 ⋅ 3 n − 1 n u n = ( − 1 ) n ⋅ sin 1 n u_n=(-1)^n\cdot \sin \frac{1}{\sqrt{n} } u n = ( − 1 ) n ⋅ sin n 1 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty }u_n ∑ n = 1 ∞ u n ∑ n = 1 ∞ u n 2 \sum_{n=1}^{\infty}u_n^2 ∑ n = 1 ∞ u n 2 ∑ n = 1 ∞ ( − 1 ) n ⋅ sin 1 n \sum_{n=1}^{\infty}(-1)^n\cdot \sin \frac{1}{\sqrt{n} } ∑ n = 1 ∞ ( − 1 ) n ⋅ sin n 1 u n = sin 1 n u n + 1 = sin 1 n + 1 u_n=\sin \frac{1}{\sqrt{n} }u_{n+1}=\sin \frac{1}{\sqrt{n+1} } u n = sin n 1 u n + 1 = sin n + 1 1 lim n → ∞ sin 1 n = 0 \lim_{n \to \infty}\sin \frac{1}{\sqrt{n} }=0 lim n → ∞ sin n 1 = 0 u n ≥ u n + 1 u_n \ge u_{n+1} u n ≥ u n + 1 ∑ n = 1 ∞ ( − 1 ) n ⋅ sin 1 n \sum_{n=1}^{\infty}(-1)^n\cdot \sin \frac{1}{\sqrt{n} } ∑ n = 1 ∞ ( − 1 ) n ⋅ sin n 1 ∑ n = 1 ∞ u n 2 = ∑ n = 1 ∞ ( sin 1 n ) 2 \sum_{n=1}^{\infty}u_n^2=\sum_{n=1}^{\infty}(\sin \frac{1}{\sqrt{n} })^2 ∑ n = 1 ∞ u n 2 = ∑ n = 1 ∞ ( sin n 1 ) 2 v n = ∑ n = 1 ∞ 1 n v_n=\sum_{n=1}^{\infty} \frac{1}{n} v n = ∑ n = 1 ∞ n 1 lim n → ∞ ( sin 1 n ) 2 1 n = lim n → ∞ 1 n 1 n = 1 \lim_{n \to \infty}\frac{(\sin \frac{1}{\sqrt{n} })^2}{\frac{1}{n} }=\lim_{n \to \infty}\frac{\frac{1}{n} }{\frac{1}{n} }=1 lim n → ∞ n 1 ( s i n n 1 ) 2 = lim n → ∞ n 1 n 1 = 1 ∑ n = 1 ∞ ( sin 1 n ) 2 \sum_{n=1}^{\infty}(\sin \frac{1}{\sqrt{n} })^2 ∑ n = 1 ∞ ( sin n 1 ) 2 ∑ n = 1 ∞ 1 n \sum_{n=1}^{\infty}\frac{1}{n} ∑ n = 1 ∞ n 1 ∑ n = 1 ∞ 1 n \sum_{n=1}^{\infty}\frac{1}{n} ∑ n = 1 ∞ n 1 ∑ n = 1 ∞ ( sin 1 n ) 2 \sum_{n=1}^{\infty}(\sin \frac{1}{\sqrt{n} })^2 ∑ n = 1 ∞ ( sin n 1 ) 2
任意项级数的绝对收敛与条件收敛 称级数∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑ n = 1 ∞ u n u n u_n u n 正,负,形式随意 为任意项级数;u n u_n u n ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑ n = 1 ∞ u n ∑ n = 1 ∞ ∣ u n ∣ \sum_{n=1}^{\infty}|u_n| ∑ n = 1 ∞ ∣ u n ∣ ∑ n = 1 ∞ ∣ u n ∣ \sum_{n=1}^{\infty}|u_n| ∑ n = 1 ∞ ∣ u n ∣ ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑ n = 1 ∞ u n ∑ n = 1 ∞ ∣ u n ∣ \sum_{n=1}^{\infty}|u_n| ∑ n = 1 ∞ ∣ u n ∣ ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑ n = 1 ∞ u n ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑ n = 1 ∞ u n ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑ n = 1 ∞ u n ∑ n = 1 ∞ ∣ u n ∣ \sum_{n=1}^{\infty}|u_n| ∑ n = 1 ∞ ∣ u n ∣ ∑ n = 1 ∞ ( ∣ u n ∣ + u n ) \sum_{n=1}^{\infty}(|u_n|+u_n) ∑ n = 1 ∞ ( ∣ u n ∣ + u n ) ∑ n = 1 ∞ ( − 1 ) n n 2 + n \sum_{n=1}^{\infty}\frac{(-1)^n}{n^2+n} ∑ n = 1 ∞ n 2 + n ( − 1 ) n ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑ n = 1 ∞ u n ∑ n = 1 ∞ u n 2 \sum_{n=1}^{\infty}u_n^2 ∑ n = 1 ∞ u n 2 ∑ n = 1 ∞ ( − 1 ) n ⋅ 1 n \sum_{n=1}^{\infty}(-1)^n\cdot \frac{1}{n} ∑ n = 1 ∞ ( − 1 ) n ⋅ n 1 ∑ n = 1 ∞ u n ≠ 0 \sum_{n=1}^{\infty}u_n \ne 0 ∑ n = 1 ∞ u n = 0 ∑ n = 1 ∞ u n \sum_{n=1}^{\infty}u_n ∑ n = 1 ∞ u n ∑ n = 1 ∞ 1 n 2 + n ∑ n = 1 ∞ 1 n 2 , P = 2 > 1 \sum_{n=1}^{\infty}\frac{1}{n^2+n}~\sum_{n=1}^{\infty}\frac{1}{n^2},P=2>1 ∑ n = 1 ∞ n 2 + n 1 ∑ n = 1 ∞ n 2 1 , P = 2 > 1 lim x → ∞ 1 n = 0 , f ( x ) = 1 x , f ′ ( x ) = − 1 x 2 < 0 \lim_{x \to \infty}\frac{1}{n}=0,f(x)=\frac{1}{x},f'(x)=-\frac{1}{x^2}<0 lim x → ∞ n 1 = 0 , f ( x ) = x 1 , f ′ ( x ) = − x 2 1 < 0 ∑ n = 1 ∞ 1 n \sum_{n=1}^{\infty}\frac{1}{n} ∑ n = 1 ∞ n 1 ∑ n = 1 ∞ u n ≠ 0 \sum_{n=1}^{\infty}u_n \ne 0 ∑ n = 1 ∞ u n = 0 lim n → ∞ u n ≠ 0 \lim_{n \to \infty}u_n \ne 0 lim n → ∞ u n = 0
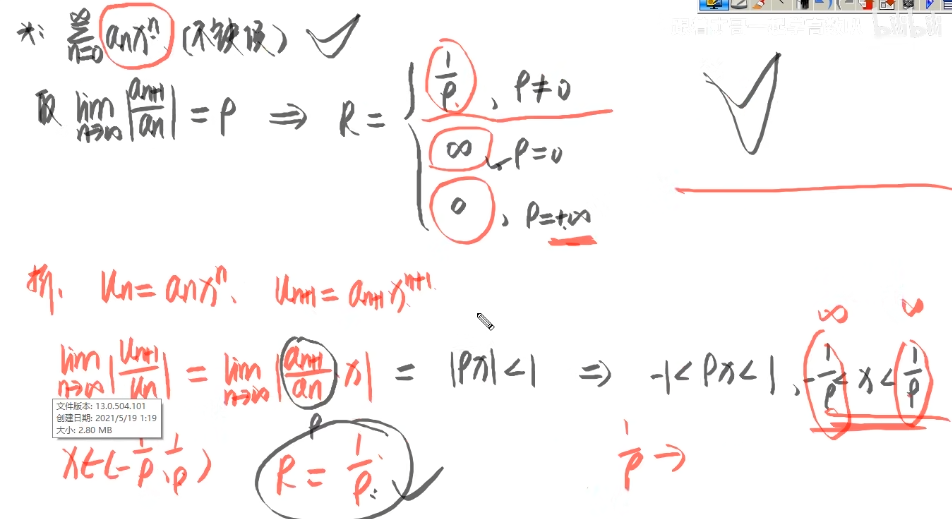
幂级数 各项均是由幂函数构成的函数项级数∑ n = 0 ∞ a n x n \sum_{n=0}^{\infty}a_nx^n ∑ n = 0 ∞ a n x n a n a_n a n x x x x n x^n x n x = x 0 x=x_0 x = x 0 ∑ n = 0 ∞ a n x 0 n \sum_{n=0}^{\infty}a_nx_0^n ∑ n = 0 ∞ a n x 0 n x 0 x_0 x 0 x = x 0 x=x_0 x = x 0 ∑ n = 0 ∞ a n x 0 n \sum_{n=0}^{\infty}a_nx_0^n ∑ n = 0 ∞ a n x 0 n x 0 x_0 x 0 x ∈ ( a , b ) x \in (a,b) x ∈ ( a , b ) x 0 x_0 x 0 a , b a,b a , b R = b − a 2 R=\frac{b-a}{2} R = 2 b − a x = a , x = b x=a,x=b x = a , x = b 收敛取闭区间,发散取开区间 ;∑ x = 0 ∞ u n ( x ) \sum_{x=0}^{\infty}u_n(x) ∑ x = 0 ∞ u n ( x ) u n , u n + 1 u_n,u_{n+1} u n , u n + 1 lim n → ∞ ∣ u n + 1 u n ∣ < 1 \lim_{n \to \infty}|\frac{u_{n+1}}{u_n}|<1 lim n → ∞ ∣ u n u n + 1 ∣ < 1 ∣ x ∣ < a ⟷ − a < x < a |x|<a \longleftrightarrow -a<x<a ∣ x ∣ < a ⟷ − a < x < a x 2 < 1 ⟷ − 1 < x < 1 x^2<1\longleftrightarrow -1<x<1 x 2 < 1 ⟷ − 1 < x < 1 lim n → ∞ ∣ u n + 1 u n ∣ < 1 \lim_{n \to \infty}|\frac{u_{n+1} }{u_n}|<1 lim n → ∞ ∣ u n u n + 1 ∣ < 1 ∑ n = 0 ∞ a n x n \sum_{n=0}^{\infty}a_nx^n ∑ n = 0 ∞ a n x n lim n → ∞ ∣ a n + 1 a n ∣ = P → x ∈ ( − 1 ρ , 1 ρ ) → R = 1 ρ \lim_{n \to \infty}|\frac{a_{n+1} }{a_n}|=P \to x \in (-\frac{1}{\rho},\frac{1}{\rho})\to R=\frac{1}{\rho} lim n → ∞ ∣ a n a n + 1 ∣ = P → x ∈ ( − ρ 1 , ρ 1 ) → R = ρ 1
具体型幂级数求解收敛区间 例题1:求幂级数∑ n = 0 ∞ n x n 3 n \sum_{n=0}^{\infty}\frac{nx^n}{3^n} ∑ n = 0 ∞ 3 n n x n u n = n x n 3 n , u n + 1 = ( n + 1 ) ⋅ x n + 1 3 n + 1 u_n=\frac{nx^n}{3^n},u_{n+1}=\frac{(n+1)\cdot x^{n+1} }{3^{n+1} } u n = 3 n n x n , u n + 1 = 3 n + 1 ( n + 1 ) ⋅ x n + 1 lim n → ∞ ∣ u n + 1 u n ∣ = lim n → ∞ ∣ ( n + 1 ) ⋅ x n + 1 3 n + 1 ⋅ 3 n n x n ∣ = lim n → ∞ ∣ ( n + 1 ) ⋅ x 3 n ∣ = ∣ x 3 ∣ < 1 \lim_{n \to \infty}|\frac{u_{n+1} }{u_n}|=\lim_{n \to \infty}|\frac{(n+1)\cdot x^{n+1} }{3^{n+1} } \cdot \frac{3^n}{nx^n}|=\lim_{n \to \infty}|\frac{(n+1)\cdot x}{3n}|=|\frac{x}{3}|<1 lim n → ∞ ∣ u n u n + 1 ∣ = lim n → ∞ ∣ 3 n + 1 ( n + 1 ) ⋅ x n + 1 ⋅ n x n 3 n ∣ = lim n → ∞ ∣ 3 n ( n + 1 ) ⋅ x ∣ = ∣ 3 x ∣ < 1 x ∈ ( − 3 , 3 ) x \in (-3,3) x ∈ ( − 3 , 3 ) R = 6 2 = 3 R=\frac{6}{2}=3 R = 2 6 = 3 x = 3 , x = − 3 x=3,x=-3 x = 3 , x = − 3 x = 3 x=3 x = 3 ∑ n = 0 ∞ n x n 3 n = ∑ n = 0 ∞ n 3 n ⋅ 3 n = ∑ n = 0 ∞ n \sum_{n=0}^{\infty}\frac{nx^n}{3^n}=\sum_{n=0}^{\infty}\frac{n}{3^n}\cdot 3^n=\sum_{n=0}^{\infty}n ∑ n = 0 ∞ 3 n n x n = ∑ n = 0 ∞ 3 n n ⋅ 3 n = ∑ n = 0 ∞ n x = − 3 x=-3 x = − 3 ∑ n = 0 ∞ n x n 3 n = ∑ n = 0 ∞ n 3 n ⋅ ( − 3 ) n = ∑ n = 0 ∞ ( − 1 ) n ⋅ n \sum_{n=0}^{\infty}\frac{nx^n}{3^n}=\sum_{n=0}^{\infty}\frac{n}{3^n}\cdot (-3)^n=\sum_{n=0}^{\infty}(-1)^n\cdot n ∑ n = 0 ∞ 3 n n x n = ∑ n = 0 ∞ 3 n n ⋅ ( − 3 ) n = ∑ n = 0 ∞ ( − 1 ) n ⋅ n x ∈ ( − 3 , 3 ) x \in (-3,3) x ∈ ( − 3 , 3 ) a n = n 3 n , a n + 1 = n + 1 3 n + 1 a_n=\frac{n}{3^n},a_{n+1}=\frac{n+1}{3^{n+1} } a n = 3 n n , a n + 1 = 3 n + 1 n + 1 lim n → ∞ ∣ a n + 1 a n ∣ = lim n → ∞ ∣ n + 1 3 n + 1 ⋅ 3 n n ∣ = lim n → ∞ ∣ n + 1 3 n ∣ = 1 3 = ρ \lim_{n \to \infty}|\frac{a_{n+1} }{a_n}|=\lim_{n \to \infty}|\frac{n+1}{3^{n+1} } \cdot \frac{3^n}{n}|=\lim_{n \to \infty}|\frac{n+1}{3n}|=\frac{1}{3}=\rho lim n → ∞ ∣ a n a n + 1 ∣ = lim n → ∞ ∣ 3 n + 1 n + 1 ⋅ n 3 n ∣ = lim n → ∞ ∣ 3 n n + 1 ∣ = 3 1 = ρ R = 1 ρ = 3 R=\frac{1}{\rho}=3 R = ρ 1 = 3 ( − 1 ρ , 1 ρ ) → x ∈ ( − 3 , 3 ) (-\frac{1}{\rho},\frac{1}{\rho})\to x \in (-3,3) ( − ρ 1 , ρ 1 ) → x ∈ ( − 3 , 3 ) x = 3 , x = − 3 x=3,x=-3 x = 3 , x = − 3 x = 3 x=3 x = 3 ∑ n = 0 ∞ n x n 3 n = ∑ n = 0 ∞ n 3 n ⋅ 3 n = ∑ n = 0 ∞ n \sum_{n=0}^{\infty}\frac{nx^n}{3^n}=\sum_{n=0}^{\infty}\frac{n}{3^n}\cdot 3^n=\sum_{n=0}^{\infty}n ∑ n = 0 ∞ 3 n n x n = ∑ n = 0 ∞ 3 n n ⋅ 3 n = ∑ n = 0 ∞ n x = − 3 x=-3 x = − 3 ∑ n = 0 ∞ n x n 3 n = ∑ n = 0 ∞ n 3 n ⋅ ( − 3 ) n = ∑ n = 0 ∞ ( − 1 ) n ⋅ n \sum_{n=0}^{\infty}\frac{nx^n}{3^n}=\sum_{n=0}^{\infty}\frac{n}{3^n}\cdot (-3)^n=\sum_{n=0}^{\infty}(-1)^n\cdot n ∑ n = 0 ∞ 3 n n x n = ∑ n = 0 ∞ 3 n n ⋅ ( − 3 ) n = ∑ n = 0 ∞ ( − 1 ) n ⋅ n x ∈ ( − 3 , 3 ) x \in (-3,3) x ∈ ( − 3 , 3 )
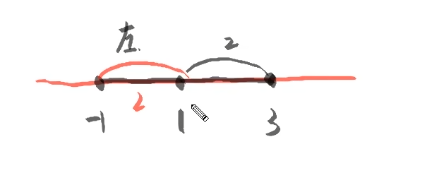
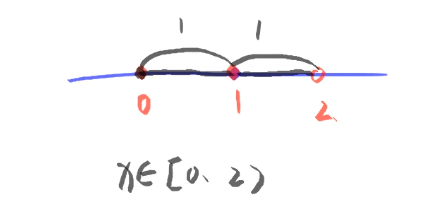
抽象型幂级数求解收敛区间 题型:求∑ n = 0 ∞ a n x n , ∑ n = 0 ∞ a n ( x − x 0 ) n \sum_{n=0}^{\infty}a_nx^n,\sum_{n=0}^{\infty}a_n(x-x_0)^n ∑ n = 0 ∞ a n x n , ∑ n = 0 ∞ a n ( x − x 0 ) n ∑ n = 0 ∞ a n x n \sum_{n=0}^{\infty}a_nx^n ∑ n = 0 ∞ a n x n x = 0 x=0 x = 0 ∑ n = 0 ∞ a n ( x − x 0 ) n \sum_{n=0}^{\infty}a_n(x-x_0)^n ∑ n = 0 ∞ a n ( x − x 0 ) n x = x 0 x=x_0 x = x 0 ∑ n = 0 ∞ a n x n \sum_{n=0}^{\infty}a_nx^n ∑ n = 0 ∞ a n x n ∑ n = 0 ∞ a n ( x − x 0 ) n \sum_{n=0}^{\infty}a_n(x-x_0)^n ∑ n = 0 ∞ a n ( x − x 0 ) n ∑ n = 1 ∞ a n ( x − 1 ) n \sum_{n=1}^{\infty}a_n(x-1)^n ∑ n = 1 ∞ a n ( x − 1 ) n x = 1 x=1 x = 1 x = − 1 x=-1 x = − 1 x = 2 x=2 x = 2 ( 1 , 3 ) (1,3) ( 1 , 3 ) x = 2 x=2 x = 2 ∑ n = 1 ∞ a n ( x − 1 ) n \sum_{n=1}^{\infty}a_n(x-1)^n ∑ n = 1 ∞ a n ( x − 1 ) n x = 0 x=0 x = 0 x = 2 x=2 x = 2 ∑ n = 1 ∞ a n x n \sum_{n=1}^{\infty}a_nx^n ∑ n = 1 ∞ a n x n x = 1 x=1 x = 1 [ 0 , 2 ) [0,2) [ 0 , 2 ) ∑ n = 1 ∞ a n x n \sum_{n=1}^{\infty}a_nx^n ∑ n = 1 ∞ a n x n x = 0 x=0 x = 0 [ − 1 , 1 ) [-1,1) [ − 1 , 1 )
幂级数的展开式
麦克劳林展开式e x = ∑ n = 0 ∞ x n n ! , x ∈ R e^x=\sum_{n=0}^{\infty }\frac{x^n}{n!},x\in R e x = ∑ n = 0 ∞ n ! x n , x ∈ R 1 1 − x = ∑ n = 0 ∞ x n , x ∈ ( − 1 , 1 ) \frac{1}{1-x}=\sum_{n=0}^{\infty }x^n,x\in (-1,1) 1 − x 1 = ∑ n = 0 ∞ x n , x ∈ ( − 1 , 1 ) l n ( 1 + x ) = ∑ n = 1 ∞ ( − 1 ) n − 1 n x n , x ∈ ( − 1 , 1 ] ln(1+x)=\sum_{n=1}^{\infty }\frac{(-1)^{n-1} }{n} x^n,x\in (-1,1] l n ( 1 + x ) = ∑ n = 1 ∞ n ( − 1 ) n − 1 x n , x ∈ ( − 1 , 1 ] 1 1 + x = ∑ n = 0 ∞ ( − 1 ) n x n , x ∈ ( − 1 , 1 ) \frac{1}{1+x}=\sum_{n=0}^{\infty }(-1)^n x^n,x\in (-1,1) 1 + x 1 = ∑ n = 0 ∞ ( − 1 ) n x n , x ∈ ( − 1 , 1 ) sin x = x − 3 3 3 ! + x 5 5 ! − … + ( − 1 ) n x 2 n + 1 ( 2 n + 1 ) ! + o ( x 2 n + 1 ) \sin x=x-\frac{3^3}{3!}+\frac{x^5}{5!}-…+\frac{(-1)^nx^{2n+1}}{(2n+1)!}+o(x^{2n+1}) sin x = x − 3 ! 3 3 + 5 ! x 5 − … + ( 2 n + 1 ) ! ( − 1 ) n x 2 n + 1 + o ( x 2 n + 1 ) cos x = 1 − x 2 2 ! + x 4 4 ! − … + ( − 1 ) n x 2 n ( 2 n ) ! + o ( x 2 n ) \cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-…+\frac{(-1)^nx^{2n}}{(2n)!}+o(x^{2n}) cos x = 1 − 2 ! x 2 + 4 ! x 4 − … + ( 2 n ) ! ( − 1 ) n x 2 n + o ( x 2 n )
幂级数的和函数带上定义域∑ n = 0 ∞ a 1 − a \sum_{n=0}^{\infty }\frac{a}{1-a} ∑ n = 0 ∞ 1 − a a 先积后导∑ n = 0 ∞ a n ⋅ x n , a n \sum_{n=0}^{\infty }a_n \cdot x^n,a_n ∑ n = 0 ∞ a n ⋅ x n , a n ( x − x 0 ) n ⇒ ∫ x 0 x S ′ ( t ) d t (x-x_0)^n \Rightarrow \int_{x_0}^{x}S'(t) dt ( x − x 0 ) n ⇒ ∫ x 0 x S ′ ( t ) d t 先积后导∑ n = 0 ∞ a n ⋅ x n , a n \sum_{n=0}^{\infty }a_n \cdot x^n,a_n ∑ n = 0 ∞ a n ⋅ x n , a n